;)
Hola Luz!
La manera mecánica de resolver inecuaciones de grado mayor que 1 es
1º buscar las raíces del polinomio P(x)=0
$$\begin{align}&x^2-8x+15=0\\&\\&x=\frac{8 \pm \sqrt{64-60}}{2}=\frac{8 \pm \sqrt{4}}{2}=\frac{8 \pm 2}{2}=\\&x_1=3\\&x_2=5\end{align}$$2º Ordenar en la recta real esas raíces , creando así los intervalos:
$$\begin{align}&(- \infty,3)\\&(3,5)\\&(5,+\infty)\end{align}$$3º Estudiar elsigno del intervalo sustituyendo un punto cualquiera del interior:
$$\begin{align}&(- \infty,3) => P(-10)=10+80+15>0 => SI\\&(3,5)=> P(4)=16-32+15=-1<0\ =>NO\\&(5,+\infty)=> P(10)=100-80+15=35>0 => SI\\&\\&Solución\\&\\&(- \infty,3) \cup (5,+\infty)\end{align}$$Con Geogebra:
A)representando la parábola y viendo sus ramas positivas:
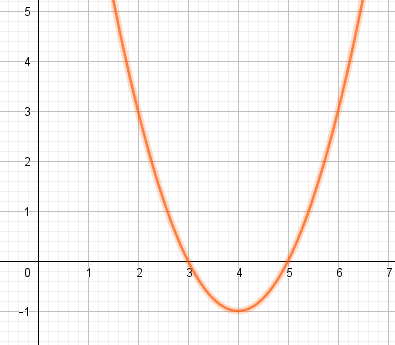
B) representando directamente la inecuación. En azul los intervalos solución
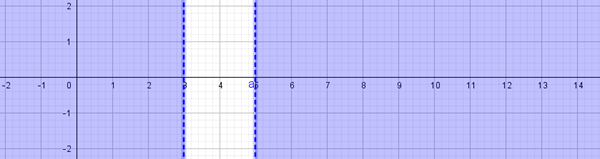
![]()


