Como resolver el siguiente ejercicio sobre un trapecio?
Se tiene un trapecio isósceles circunscrito a una circunferencia, cuya base menor mide "a" unidades de longitud y base mayor "b" unidades de longitud. Calcular la longitud del segmento de recta de extremos en los puntos de tangencia de la circunferencia con los lados oblicuos.
1 respuesta
Respuesta de Lucas m
1
;)
Hola Sofia Maldonado!
Bonito problema.
La situación es la siguiente:
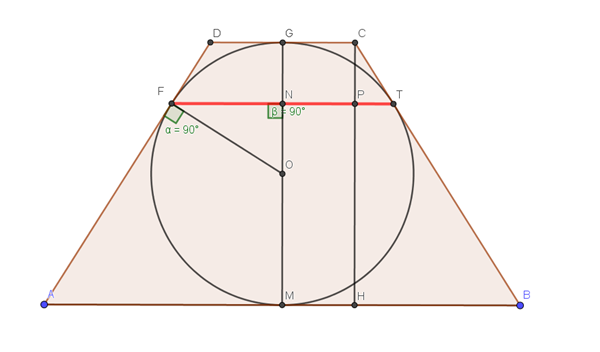
DC=a
AB=b OG=OM=OF= r
CH=GM=2r
Teorema de la tangente: BT=BM= b/2
Teorema de la tangente: CT=CG=a/2
==> BC=BT+CT= (a+b)/2
Pitágoras en CHB:
$$\begin{align}&CB^2=CH^2+HB^2\\& \frac{(a+b)^2}4=(2r)^2+HB^2\\&\\&HB= \frac {b-a}2\\&\\&\frac{(a+b)^2}4=(2r)^2+ (\frac {b-a}2 )^2\\&\\&\frac{a^2+2ab+b^2} 4=4r^2+ \frac{a^2-2ab+b^2}4\\&\\&16r^2=4ab\\&\\&r= \frac{\sqrt{ab}}2\\&\\&Semejanza \ triángulos \ CPT \equiv CHB:\\&\frac{CP}{CH}= \frac{CT}{CB}\\&\\&CP=CH \frac{CT}{CB}=2r \frac{\frac a 2}{\frac{a+b} 2}= \sqrt {ab} \frac a {a+b}=GN\\&==>\\&ON=OG-GN=r-GN= \frac{ \sqrt {ab}} 2-\frac{a \sqrt{ab}}{a+b}= \sqrt{ab} ( \frac 1 2- \frac a {a+b})\\&\\&Pitágorasº triángulo \ ONF:\\&OF^2=FN^2+ON^2\\&FN^2=OF^2-ON^2=r^2-ON^2= \frac {ab} 4- \Bigg( \sqrt{ab} ( \frac 1 2- \frac a {a+b}) \Bigg)^2=\\&\\&= \frac {ab} 4- ab \Big( \frac 1 4- 2 \frac 1 2 \frac a {a+b}+ \frac{a^2}{(a+b)^2} \Big)= \\&\\&ab \Big( \frac 1 4- \frac 1 4+ \frac a {a+b}- \frac{a^2}{(a+b)^2} \Big)=\\&\\&ab \Big( \frac a {a+b}- \frac{a^2}{(a+b)^2} \Big)=ab \frac{a(a+b)-a^2}{(a+b)^2}=\\&\\&ab \frac{a^2+ab-a^2}{(a+b)^2}= \frac{(ab)^2}{(a+b)^2}\\&\\&FN= \frac{ab}{a+b}\\&\\&FT=2FN= \frac{2ab}{a+b}\end{align}$$Saludos
;)
||*||
¡Gracias!
Guau!
No creí que fuera así de complicado
Pero muchas gracias
Te agradezco por tu tiempo (;
