;)
Hola Sofia!
Tal como yo lo veo la superficie cónica parcial, intersección entre el cono (grande) y la esfera es la superficie lateral del tronco de cono determinado por el cono grande menos el cono amarillo.
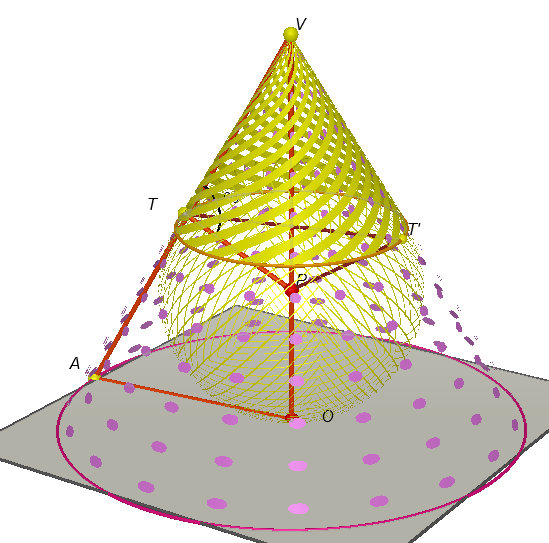
Q , que no se ve , es el punto medio de TT'
QT=s (radio circunferencia superior del tronco)
AO=10
VO=24
r=AO=10
R=PT (radio esfera)
Area lateral tronco cono:
$$\begin{align}&A_l= \pi(r+s)g\\&\\&triagulos \ semejantes:\\&VTP \equiv VOA\\&angul\ V \ común\\&T=O=90º\\&==>\\&P=Aº (suman 180º)\\&\\&\frac{VT}{VO}=\frac{PT}{OA}\\&\\&\frac{VT}{24}= \frac{R}{10} \ ==> VT= \frac {12}5 R\\&\\&Pitágoras \ VTP\\&VP^2=PT^2+VT^2\\&\\&(24-R)^2=R^2+(\frac {12}5 R)^2\\&\\&576-48R+R^2=R^2+ \frac{144}{25}R^2\\&multiplicando \ por \ 25\ y \ reordenando\\&\\&144R^2+1200R-14400=0\\&R= \frac{20}3\\&\\&Teorema\ del \ cateto\ en VTP\\&PT^2=VP·QP\\&(\frac{20}3)^2=(24- \frac{20} 3)·QP\\&\\&QP= \frac{400}{156}=\frac{100}{39}\\&\\&Pitágoras\ en TQP:\\&PT^2=QT^2+QP^2\\&\\&QT^2=( \frac{20} 3)^2-(\frac{100}{39})^2= \frac{6400}{169}\\&\\&QT= \frac{80}{13}\\&QT=s\\&g=VA-VT\\&\\&\\&Semejanza: VTQ \equiv VAO\\&\frac{VT}{VA}=\frac{QT}{OA}\\&\\&\frac{VT}{26}= \frac{QT}{10}\\&\\&VT=\frac{26}{10}QT=\frac{13}{5} \frac {80}{13}=16\\&\\&g=TA=VA-VT=26-16=10\\&\\&VA=pitágoras=\sqrt{10^2+24^2}=26\\& \\&A_{tronco_con}= \pi(r+s)g= \pi(10+ \frac{80}{13})10= \frac{2100}{13} \pi \ cm^2=507.488\\&\end{align}$$Saludos y menudo problemita!!
;)
;)


