Como determinar el MCD de 126, 48, 60, y usando descompocicion factorial determine el MCM Y el MCD 14, 28,7,21, 12

$$\begin{align}&126=2*3^2*7\\&48=2^4*3\\&60=2^2*3*5\end{align}$$

Hola Jose Lopez

Para resolver tus ejercicios lo primero que debemos tener claro es que para determinar tanto el MCD (Máximo Común Divisor) como el mcm (mínimo común múltiplo), debes primero descomponer cada uno de los números en sus factores primos.

Determinación del MCD de 126, 48 y 60

* Descompongamos el 126

126 / 2 =63

63/3 = 21

21/3=7

7/7=1

Lo escribimos de esta forma

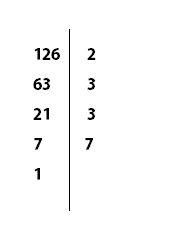
Por lo tanto 126=2*3*3*7 = 2*3^2*7 (donde el símbolo ^ indica que es una potencia) 

Ahora, repetimos el procedimiento y descomponemos los otros números

$$\begin{align}&48=2^4*3\\&60=2^2*3*5\end{align}$$

Ya que descompusimos los tres números determinamos el MCD (Máximo Común Divisor), ¿Cómo? La regla dice que son LOS COMUNES CON SU MENOR EXPONENTE, primero determino los comunes, que son el 2 y el 3

$$\begin{align}&126={\color {blue}2}*{\color {red}{3^2}}*7\\&48={\color {blue}{2^4}}*{\color {red}{3}}\\&60={\color {blue}{2^2}}*{\color {red}{3}}*5\\&\\&\end{align}$$

Y luego de ellos tomo su menor exponente, en el caso del 2 el menor exponente es 1 (en 126) y en el caso del 3 el menor exponente es 1 en 48 y 60, por lo tanto:

$$\begin{align}&126={\color {blue}2}*{\color {black}{3^2}}*7\\&48={\color {black}{2^4}}*{\color {red}{3}}\\&60={\color {black}{2^2}}*{\color {black}{3}}*5\\&\\&MCD(126,48,60)=2*3=6\end{align}$$

Determinación del mcm y MCD de 14, 28, 7, 21 y 12

El procedimiento para el MCD es ya esta expuesto arriba. Para la determinación del mcm (mínimo común múltiplo), utilizas la descomposición en números primos pero esta vez hallas LOS COMUNES Y NO COMUNES CON SU MAYOR EXPONENTE

Los resultados son:

MCD(14, 28, 7, 21, 12)=1

mcm(14, 28, 7, 21, 12)=84

Coméntame si tienes algún problema para llegar a estos resultados.

Puedes ver videos como:

https://www.youtube.com/watch?v=YHdlZlRq_qM 

https://www.youtube.com/watch?v=kxDeTxbnk-c 

Éxitos