La recta l1 pasa por los puntos (-2, 3) y (4, -1)

Saludos Angélica castaño

Primero se analiza toda la recta, hallando la ecuación que la define, para lo cual hallo su pendiente m y su punto de corte b

$$\begin{align}&m=\frac{\Delta y}{\Delta x} = \frac{y_2-y_1}{x_2-x_1}= \frac{-1-3}{4-(-2)}=\frac{-4}{6}=\frac{-2}{3}\\&\\&\\&y=mx+ b\\&\\&se\ sustituye \ el \ valor\ de \ m\ obtenido\\&\\&y=\bigg (\frac{-4}{6}\bigg)x+ b\\&\\&se\ sustituye \ el \ valor\ de \ un\ punto\ \\&\\&3=\bigg (\frac{-4}{6}\bigg)(-2)+ b\\&\\&\\&3=\bigg (\frac{8}{6}\bigg)+ b\\&\\&\\&b=3-\bigg (\frac{8}{6}\bigg)\\&\\&\\&b=\frac{18-8}{6}\\&\\&\\&b=\frac{10}{6}= \frac{5}{3}\\&\\&\\&\\&\\&\end{align}$$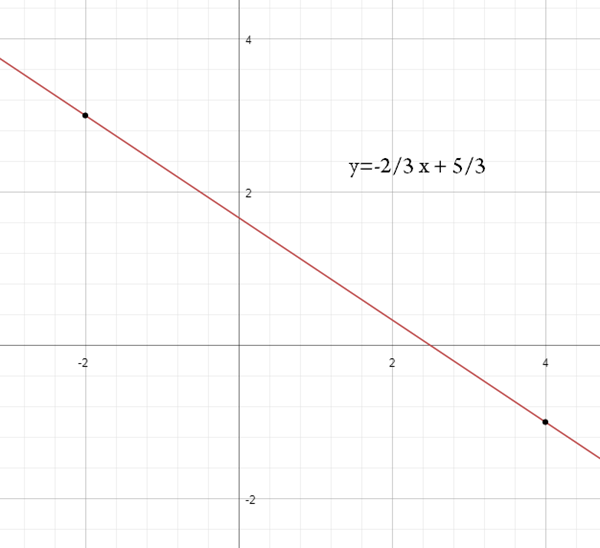

a.

Pendiente: m=-2/3

Ecuación de la recta: y=-2/3 x + 5/3

b. Intercepto en y: b=5/3

c. Intercepto en x:

Empleando la ecuación de la recta, se evalua x para y=0

$$\begin{align}&y=-\frac {2}{3} x+\frac {5}{3}\\&\\&\\&0=-\frac {2}{3} x+\frac {5}{3}\\&\\&\\&-\frac {2}{3} x=-\frac {5}{3}\\&\\&\\&\\& x=-\frac {5}{3} \bigg(  -\frac {3}{2}                        \bigg)\\&\\&\\& x=\frac {5}{2}\end{align}$$

d. Decreciente porque la pendiente es negativa

e.  Se evalúa el valor de y para x=-7

$$\begin{align}&y=-\frac {2}{3} x+\frac {5}{3}\\&\\&\\&y=-\frac {2}{3} (-7)+\frac {5}{3}\\&\\&\\&y=\frac {14}{3} +\frac {5}{3}\\&\\&\\&y=\frac {14+5}{3} \\&\\&\\&y=\frac {19}{3}  =  6,33\\&\end{align}$$

Como para x=-7 , y=19/3=6,33 y no -3, el punto (-7, -3) no pertenece a la recta

f. Listo