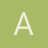Como se resuelve este no sé si es una desigualdad yo las he resuelto pero con números demostración no se como
Si. A, b >=0 mostrar que a<b <-------->a^2 < b^2<------->raíz de a <raíz de b
2 respuestas
$$\begin{align}&a < b\end{align}$$Si multiplicamos la inecuación por un número positivo (por ejemplo, a ó b), el signo la desigualdad no cambia:
$$\begin{align}&a < b\\&a·a < a·b\\&a^2 < a·b\\&a^2 < a·b < b·b = b^2 \\&a^2 < b^2 \end{align}$$En la penúltima desigualdad, como b>a, entonces b·b es mayor que a·b.
Con lo visto, ya se demuestra lo de las raíces. Usaremos, pues
$$\begin{align}&a< b \Leftrightarrow a^2 < b^2 \end{align}$$Cambiamos a y b por sus raíces:
$$\begin{align}&\sqrt{a} < \sqrt{b} \Leftrightarrow \\&(\sqrt{a})^2 < (\sqrt{b})^2 \Leftrightarrow\\&a < b\\&\end{align}$$
También puedes poner las dos variables en función de un numero.
Si el texto te dice que la desigualdad A<B debe ser cierta para cualquier numero mayor o igual que cero, entonces podriamos llamar "n" a este mumero y expresarl laquesigualdad basica en funcion de el:
En A<B hariamos A=n y para mantener la deaigualdad, B=n+1.
Con esto nos vamos a nuestra primera condición a demostrar:
A^2<B^2. Sustituimos el numero n
n^2<(n+1)^2. Desarrollamos el bonomio: n^2< n^2+2n+1. Pasamos n^2 hacia la izquierda n^2-n^2<2n+1 realizamos la operacion de resta: 0<2n+1. Y he aquí la demostración, ya que la desigualdad se mantiene para cualquier valor de n mayor o igual a cero.
Para la raíz cuadrada de A<raiz cuadrada de B. Tenemos que recordar que elevar un valor a la potencia 1/2 es igual a la raiz cuadrada de ese valor. Así que la inecuación queda: A^(1/2)<B^(1/2) y sustituyendo nuestro numero: n^(1/2)<(n+1)^(1/2) ahora recordemos tambien que si un numero elevado a una potencia lo elevamos a otra, la potencia resultante a la que se elevara ese numero es la multiplicacion de las dos potencias. Así que elevamos nuestra inecuación al cuadrado: (n^(1/2))^2<((n+1)^(1/2))^2. Con lo que se cancela el 1/2 o el radical y nos queda; n<n+1. Pasamos n a la izquierda del signo n-n<1 realizamos la resta y nos queda 0<1 . lo cual no admite duda alguna de que sea cierto y queda demostrada la desigualdad.