¿Por qué se dice que el seno y el coseno son el inverso del angulo?
algo que nunca comprendí..., ¿Por qué se llama al coseno, el seno y la tangente inverso u opuesto al angulo? El coseno dice cuantas veces el radio del circulo entra en el cateto adyacente del triangulo ... Pero no entiendo porque se le llama inverso u opuesto al angulo
2 Respuestas
Parece que hay una pequeña confusión como un juego de palabras. Analicemos por partes lo que dices:
El coseno dice cuantas veces el radio del circulo entra en el cateto adyacente del triangulo
No es del triángulo, sino del ángulo (central), esto sería lo correcto
El coseno dice cuantas veces el radio del circulo entra en el cateto adyacente al ángulo central
Ahora expliquemos esa enredadera del inverso.
1) Coseno es una función que viene definida de la siguiente forma
$$\begin{align}&\cos : \mathbb{R}\to [-1,1]\end{align}$$Cuyas propiedades son las conocidas:
1.1) es una función periódica
$$\begin{align}&\cos(x+2\pi)=\cos x\end{align}$$1.2) Si le hacemos una traslación es igual a la función seno
$$\begin{align}&\cos(x-\frac{\pi}{2})=\sin x\end{align}$$1.3) Es continua en toda la recta real.
1.4) Es continuamente diferenciable en todo R
$$\begin{align}&\dfrac{d\cos x}{dx}=-\sin x\end{align}$$Y así podemos continuar con más propiedades...
Luego debemos recordar que algunas funciones tienen inversa, así por ejemplo la función inversa de
$$\begin{align}&f(x)=x^3\end{align}$$es
$$\begin{align}&g(x)=\sqrt[3]x\end{align}$$ya que la composición de ambas funciones nos da la función identidad
$$\begin{align}&f\circ g(x)=g\circ f(x)=x\end{align}$$para cualquier x real. Sin embargo hay funciones que tienen inversa con ciertas restricciones, como por ejemplo
$$\begin{align}&h(x)=x^2\end{align}$$Cualquiera sospecharía que la función inversa de h es
$$\begin{align}&j(x)=\sqrt{x}\end{align}$$Pero en este caso el dominio de j son todos los reales NO negativos, por eso j no es la inversa de h, pero si hacemos un ajuste como este
$$\begin{align}&h_1(x)=x^2~,~ \forall x\in [0,+\infty)\end{align}$$entonces h1 si es la inversa de j para los número reales no negativos.
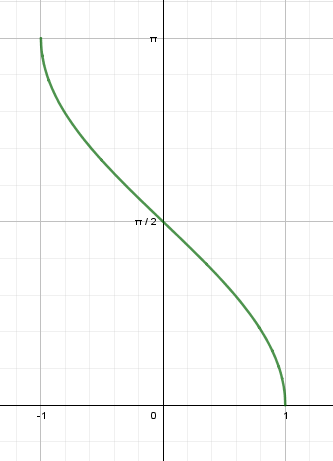
2) Ahora como coseno es una función sospecharíamos que esta debe tener una inversa, si no en todo su dominio, al menos en una parte de este. En efecto se definirá la inversa del coseno como arcocoseno de la siguiente forma
$$\begin{align}&\arccos: [-1,1]\to[0,\pi]\end{align}$$Donde
$$\begin{align}&\arccos (\cos x)=x~,~\forall x\in[0,\pi]\\&\\&\cos (\arccos \chi) =\chi ~.~ \forall \chi\in[-1,1] \end{align}$$Veamos las gráficas
Gráfica de la función coseno
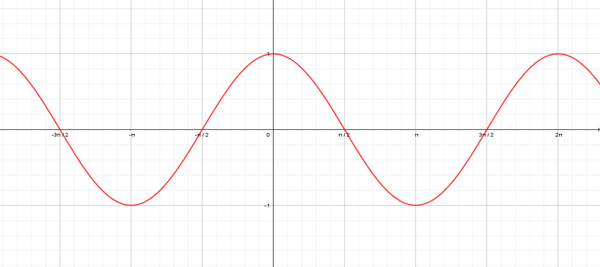
Ahora solo centrémonos en el dominio [0, pi]
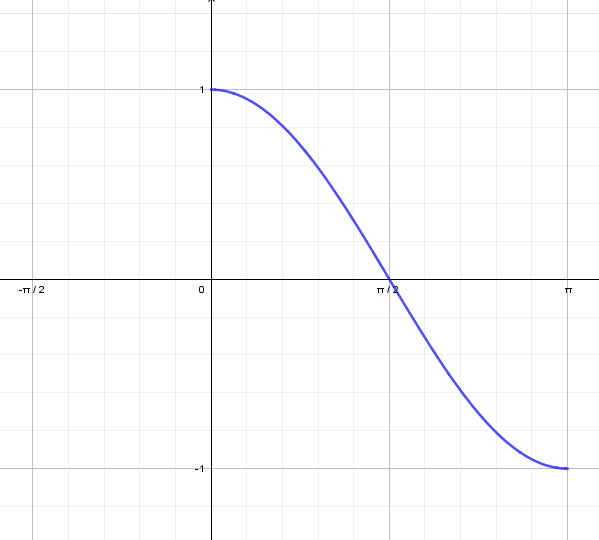
Luego la función arccoseno
¿A dónde dice eso?
Perdón, me euivoque.., quise decir que se dice que el angulo seria el inverso u lo opuesto al coseno..., un profeesor ena vez me dijo que si quieres hallar el angulo con el coseno, tienes que hacer en la calculadora.., el inverso del coseno o arcoseno pero no entendí eso
Claro. Lo que pasa es que al tocar la tecla shift de la compu el display te devuelve la función origen: O sea si tienes cos alfa = 0.707 y pulsas shitf 7 te entrega el angulo alfa = 45 °. Pero la inversa aritmética de (cos alfa) es (1 / cos alfa) en ese caso seria 1.4144... nada que ver con el angulo alfa.
Igualmente en álgebra se suele escribir (cos alfa)^-1 como igual al angulo alfa y así lo estaría interpretando la compu. Comprendes.?
la verdad que no....no entiendo porque al angulo es el inverso del coseno
El inverso de la función cos alfa = arc. Cos alfa ... y así lo interpreta la calculadora cuando pulsas el shift. El inverso aritmético seria (1/ cos alfa) que no tiene nada que ver.
Pero la funcion (arc. Cos alfa)tambien se escribe como(cos alfa)^-1... de ahi la confusion.
si ............., yo entiendo eso..............., pero lo que no comprendo es porque se le llama al angulo el inverso del coseno...¿por que es el inverso?
Porque lo anotan como (cos alfa)^-1.
Sencillamente se llama inverso del coseno porque se anota como (cos alfa)^-1.
Pero (cos alfa)^-1 vendría a ser lo mismo que (1/ cos alfa)
Y ud dice que que no tiene nada que ver.
Claro. Para las funciones trigonométricas de un angulo, sen, cos, tg . ...se llama "invertirla" volver al angulo de origen . Invertir una de estas funciones significa devolver el angulo.
Ejemplo: si tenes y= sen x = 0.866 ....la funcion inversa se llama arc. sen x = arc.sen (0.866) =60°. Esto lo haces anotando el nro. 0.866 en la calculadora y luego shift sen ... En muchos textos te ponen arc. Sen x = (sen x)^-1 ... pero lo correcto es escribirla como arc. Sen x. Así lo hago yo y lo enseño a los alumnos.
La función inversa aritmética del (sen x) seria = (sen x)^-1= (1/sen x) ... se denomina cosecante x ... y es otra función trigonometrica del angulo x . Te lo aclaro extensamente Karl Mat en su respuesta.