Como encontrar su gráfica y ecuación de una circunferencia

Primero tendrás que encontrar las coordenadas del punto de cruce, para lo cual resuelves las exuaciones de manera simultanea:

X+3Y+3=0

X+Y+1=0

Resolviendo para "X", "Y" tendrás la coordenada (0, -1).

Ahora sabemos que la ecuación para la circunferencia de centro (a, b) y radio "r" es:

$$\begin{align}&(X-a)+(Y-b)=r^2\\&\end{align}$$

Sustituye los valores del centro, del radio y obtendras la ecuacion buscada.

Intentalo, y si tienes problemas, avisame.

_

La fórmula que plantea Pilar Valenzuela esta mal.

1. Encontrar su gráfica, es simplemente despejar la variable "y" de ambas ecuaciones.

$$\begin{align}&x+3y+3=0\end{align}$$

$$\begin{align}&(1)\rightarrow y=\frac{-1x}{3}-1\end{align}$$

Y la otra:

$$\begin{align}&x+y+1=0\end{align}$$

$$\begin{align}&y=-x-1\end{align}$$

Por lo que la gráfica de intersección de ambas rectas para obtener el centro es:

$$\begin{align}&C(h;k)\rightarrow C(0;-1)\end{align}$$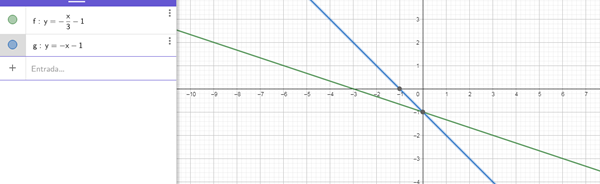

Y reemplazando en la ecuación de la circunferencia:

$$\begin{align}&(x-h)^2+(y-k)^2=r^2\end{align}$$

Sabiendo que "r" (radio) es igual a 6, reemplazamos en la ecuación y obtenemos:

$$\begin{align}&(x-0)^2+(y-(-1))^2=6^2\end{align}$$

$$\begin{align}&x^2+(y+1)^2=36\end{align}$$