Como encontrar las ecuaciones de los lados de un triangulo?

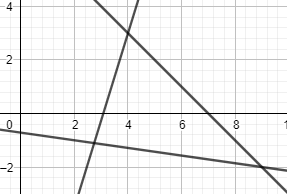
Para este problema seguro que te resulta más fácil ir dibujando cada, puedes usar una herramienta como https://www.math10.com/en/geometry/geogebra/geogebra.html Si dibujas los datos que te dan verás esto:

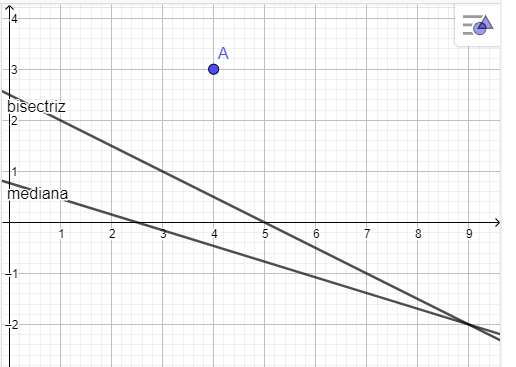
Como ves la mediana y la bisectriz se tocan en un vertice y si resolvemos el sistema de ecuaciones comprobamos que B(9,-2) Y ahora es sacar la recta AB x-y-7=0

Ahora utilizando la mediana y A podemos obtener la recta AC ya que sabemos que la perpenticular a la mediana que pase por A será la recta.

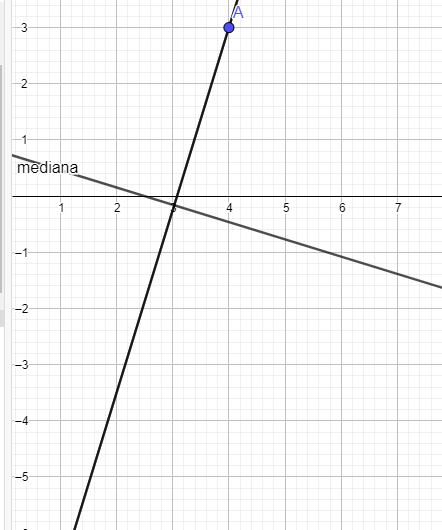
Por tanto cogemos la pendiente de la mediana (4/13) hacemos la pendiente tangente (-13/4) y construimos una recta que pase por (4,3) y nos quedaría una ecuación -13x + 4y -40 = 0

Y ahora viene la parte que creo que es más dificil. Tenemos la bisectriz, y sabemos que la distancia desde un punto de esta (B') a otro del lado AB (X') será la misma que desde B' a un punto de la recta AC (X'') y que la distancia desde X'' a B será igual que la distancia desde X' a B. Con eso tenemos un sistema de ecuaciones (de segundo grado con 2 incognitas) que podremos resolver. En mi caso para B' he usado 5,0 y para X' 6,1. Al final lo que intentamos resolver es el otro punto en el que se tocan las circunferencias formadas en los centros B y B' con radios hasta X'

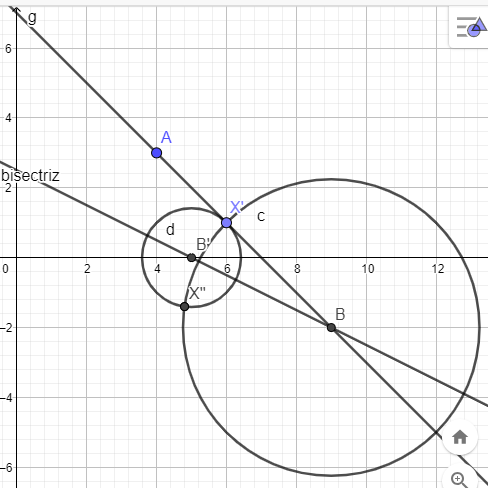
Sí calculas las distancias te saldrá 

$$\begin{align}&\sqrt 2\end{align}$$

y 

$$\begin{align}&\sqrt 18\end{align}$$

ahora resuelves el sistema de ecuaciones 

$$\begin{align}&\sqrt (2) = \sqrt((x-5)^2 + y^2)\\&\sqrt (18) = \sqrt((x-9)^2+(y+2)^2) \end{align}$$

este sistema no te va a dar un valor si no una función, que es la recta que pasa entre X' y X'' y=2x-11

Y ahora solo te queda sustituir esa y en cualquiera de las funciones de la circunferencia la cual te saldrá una ecuación de segundo grado cuyos valores de x serán 6 o 4.8. 6 es el punto que ya tienes por tanto resuelves la y con x=4.8 y te dará -1.4 ahora con ese punto y el punto B sacas la recta BC: 0.6x+4.2y+3=0

Y ya tienes las 3 rectas