Hallar la Ecuación General de La Parábola.

Primero es bueno ver que es lo que nos están pidiendo, esta es más o menos la gráfica de la parábola que nos están pidiendo. Nos están dando los puntos extremos del lado recto.

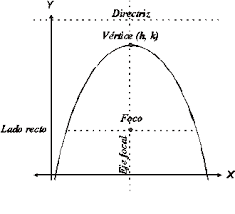
primero hallamos la distancia entre los puntos del lado extremo

$$\begin{align}&d_{pq}=\sqrt{(5-1)^2+(2-2)^2}=4\end{align}$$

esta distancia es 2 veces el parametro p,es decir, 2p, la distancia entre el foco y los puntos extremos del lado recto es p, entonces si 2p=4, p=2. Ahora como ves en la imagen el foco se encuentra a la derecha del punto P  2 unidades y a la izquierda del punto Q 2 unidades. Es indiferente cual punto uses, yo voy a usar el punto P, pero si fueras a usar Q debes restarle 2 unidades al valor de x

$$\begin{align}&F=(1+2,2)\\&F=(3,2)\end{align}$$

Ademas la distancia del vértice al foco es p/2, osea 1

Y en la imagen vemos que el vértice debe de estar arriba del foco. Y debe estar arriba 1 unidad

V=(3,2+1)=(3,3)

Como es una parabola vertical su ecuacion es de la forma

(x-h)^2=4p(y-k)^2

Donde h y que son las coordenadas en por y y del vértice respectivamente, y como la parábola va hacia abajo se coloca un negativo en el 4p

La ecuación seria

(x-3)^2=-8(y-3)^2