Rango y asíntotas de esta función

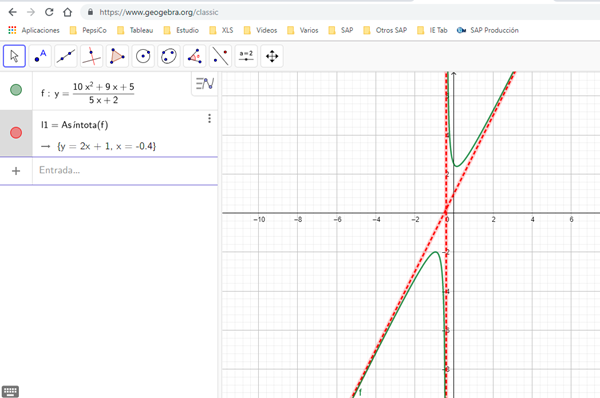
La función está definida para todos los puntos, excepto donde el denominador sea 0, o sea

5x + 2 = 0

x = -2/5

En ese punto la función no está definida, en el resto de los valores sí y vemos que pasa en ese punto si nos acercamos por derecha o por izquierda

$$\begin{align}&\lim_{x \to -2/5}\frac{10x^2+9x+5}{5x+2} \to \infty\\&\text{Solo me voy a concentrar en el signo del numerador y denominador dependiendo por donde nos acerquemos,}\\&\text{ya que en ese punto se que tenderá a infinito, lo que me interesa es ver si será el positivo o el negativo}\\&\lim_{x \to -2/5^-}\frac{10x^2+9x+5}{5x+2} \to \frac{+}{0^-}\to-\infty\\&\lim_{x \to -2/5^+}\frac{10x^2+9x+5}{5x+2} \to \frac{+}{0^+}\to+\infty\\&\text{En principio el rango de la función es R, veamos si hay algún valor para el que no está definido}\\&\text{Para eso hallamos }y^{-1}\\&y=\frac{10x^2+9x+5}{5x+2}\\&y(5x+2)=10x^2+9x+5\\&5yx+2y-10x^2-9x=5\\&-10x^2+(5y-9)x=5-2y\\&-10x^2+(5y-9)x+2y-5=0\\&\text{Vemos que quedó una expresión cuadrática para x. Para encontrar para que valores está definida (usar Bhaskara)}\\&\text{Tenemos que ver que el discriminante sea mayor o igual que cero}\\&\text{En otras palabras, tenemos que:}\\&a=-10\\&b=5y-9\\&c=2y-5\\&\text{Tenemos que ver que }b^2-4ac\ge0 \Rightarrow\\&(5y-9)^2-4\cdot (-10)\cdot (2y-5) \ge 0\\&25y^2-90y+81+80y-200 \ge 0\\&25y^2-10y+-119 \ge 0\\&\text{Vemos que es una parábola con las ramas hacia arriba (el coeficiente principal es >0), así que}\\&\text{Entre las raíces será negativo y para el resto será positivo}\\&\text{Calculando las raíces de y, tenemos}\\&y_{1,2}=\frac{10\pm \sqrt{(-10)^2-4\cdot 25 \cdot (-119)}}{2\cdot 25}\\&y_1 \approx -1.99\\&y_2 \approx 2.39\\&\text{O sea que el rango de la función será}\\&(-\infty, -1.99] \cup[2.39, \infty)\end{align}$$

Te dejo el gráfico con la verificación

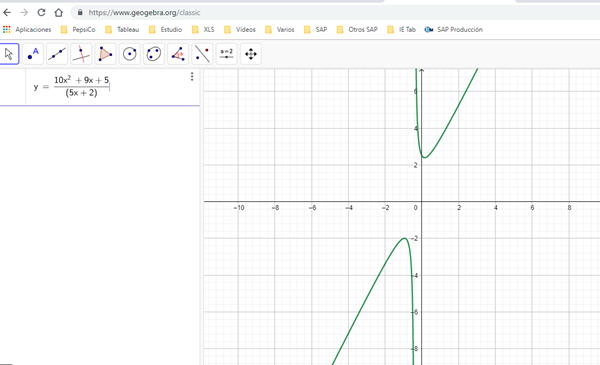
y el agregado de las asíntotas