Una catedral se encuentra sobre una colina, Cuando se observa la parte superior del campanario desde la base

Andrea, en este tipo de ejercicio lo primero que conviene hacer es un esquema con la información que tenemos para ayudar a interpretar los datos, y así vemos que información tenemos y que nos puede llegar a faltar.

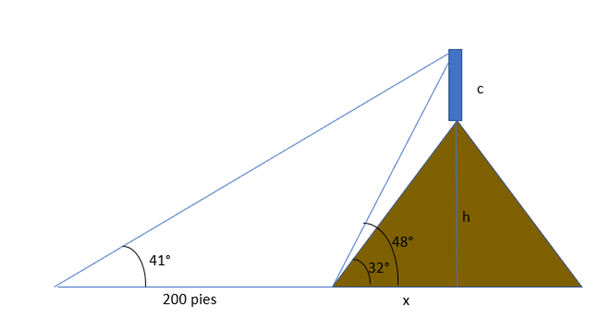
En esencia nos piden c (altura de la catedral), h (altura de la colina), y no lo están pidiendo, pero por las dudas marqué x (mitad de la base de la base de la colina).

Ahora usemos las funciones trigonométricas a ver que podemos hallar...

$$\begin{align}&tan(41°) = \frac{c+h}{200+x}\\&tan(48°)=\frac{c+h}{x}\\&\text{En ambas expresiones tenemos 'c+h', así que podemos igualarlas}\\&tan(41°)(200+x) = tan(48°)(x)\\&0.87(200+x)=1.11x\\&174 + 0.87x = 1.11x\\&174 = 0.24x\\&x=725\\&\text{Ahora usemos los ángulos que se forman en la base de la colina}\\&tan(32°) = \frac{h}{x} \\&tan(48°)=\frac{c+h}{x}\\&\text{Tenemos x en ambas expresiones, así que despejamos e igualamos...}\\&\frac{h}{tan(32°)} = \frac{c+h}{tan(48°)}\\&\text{Vemos que tenemos una ecuación con 2 incógnitas, \sin embargo también tenemos la expresión del ángulo de 41°}\\&tan(41°) = \frac{c+h}{925} \to c+h=tan(41°) \cdot 925\\&\text{Reescribo la expresión anterior}\\&\frac{h}{tan(32°)} = \frac{c+h}{tan(48°)}=\frac{tan(41°)\cdot 925}{tan(48°)}\\&\text{Me quedo con la primer y última expresión}\\&h = \frac{tan(41°)\cdot 925 \cdot tan(32°)}{tan(48°)}\\&h = 452.41 \text{  (altura de la colina)}\\&\text{Uso cualquier expresión para hallar 'c', en particular}\\&c+h=tan(41°)\cdot 925\\&c=0.87 \cdot 925 - 452.41\\&c = 353.34 \text{  (altura de la catedral)}\end{align}$$

Como ves, no es complicado, pero la imagen ayuda mucho a entender y lo importante es ir 'paso a paso'

Salu2