Alguien que me ayude con unos ejercicios de física para salvar el semestre

Es un ejercicio bastante interesante ya que mezcla varios de los conceptos de física.

Lo primero es hacer un esquema de la información que tenemos... ( albert buscapolos Ing°, sentite libre de usarlo, porque tus conocimientos en física son muy superiores a los míos :-) y seguramente darás una mejor solución)

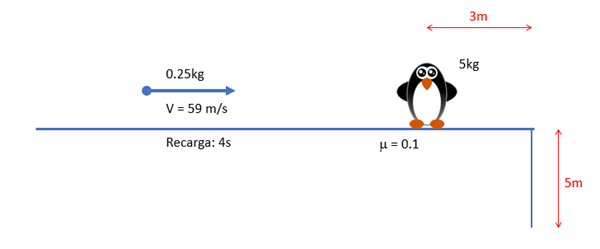
Lo primero que noto es que los 5m del precipicio no sirven para nada (solo para indicar que debe llegar hasta ahí).

Lo otro es que básicamente el problema se resume en calcular cuanto tarda el pingüino (con la fecha clavada) en recorrer esos 3m que lo separan del precipicio (si es que llega, ya veremos por que)

Lo primero es calcular a que velocidad se movería el pingüino hacia el precipicio al recibir el flechazo. Como la flecha queda clavada al pingüino, podemos decir que se trata de un choque perfectamente plástico y por tanto se conserva la energía cinética del sistema

$$\begin{align}&m_f v_f^2 + m_pv_p^2 = (m_f+m_p)v^2\\&0.25 \cdot 59^2 + 5 \cdot 0^2 = (0.25+5)v^2\\&v=\sqrt{\frac{870.25}{5.25}}\\&v=12.87 \ m/s\\&\end{align}$$

Ya sabemos que el pingüino con la flecha clavada se comienza a mover hacia la derecha (precipicio) a una velocidad de 12.87 m/s

Ahora hagamos el DCL del pingüino con la flecha para ver las fuerzas intervinientes...

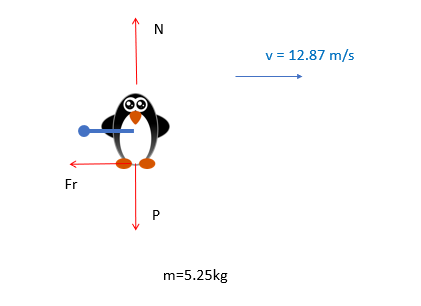
Vemos que hay 3 fuerzas intervinientes, el peso, la normal (en el eje Y), y la fuerza de rozamiento en el eje X (que intenta detener al pingüino)

En el eje Y tenemos que las fuerzas P, N se netean (no se está moviendo en esa dirección) y cada una vale 51.45N

Luego tenemos que

$$\begin{align}&F_r= \mu N\\&F_r = 0.1 \cdot 51.45N\\&F_r = 5.15N\\&\text{Sabemos que se está frenando en el eje X, así que calculamos}\\&F_r = m \cdot a\\&5.15 = 5.25 \cdot a\\&a = -9.8 m/s^2\\&\text{Le puse el signo negativo porque sabemos que se está frenando el cuerpo, }\\&\text{así que actua en sentido opuesto al desplazamiento}\end{align}$$

Finalmente planteamos la expresión de MRUA

$$\begin{align}&x(t)=x_0 + v_0 \cdot t + \frac{1}{2} a \cdot t^2\\&Reemplazando\\&x(t)=12.87 \cdot t -4.9 \cdot t^2\\&\text{Veamos cuanto tarda para recorrer los 3 m}\\&3=12.87 \cdot t -4.9 \cdot t^2\\&\to\\&0=-3+12.87 \cdot t -4.9 \cdot t^2\\&\text{Planteando la resolvente}\\&t_1=0.26s\\&t_2=2.37s\end{align}$$

Tarda menos de 4s en recorrer los 3m por lo que el pingüino se salva

Salu2

Creo que la respuesta que te dí está incompleta porque el resultado plantea 2 tiempos posibles, cuando en realidad esto no será así y voy a explicarlo.

Antes de aclarar ese punto, veamos en que momento la velocidad se hace 0, retomando la expresión de posición

x(t) = 12.87t - 4.9 t^2

Por lo tanto la velocidad será

v(t) = 12.87 - 9.8 t

y finalmente la velocidad será 0 para

0 = 12.87 - 9.87t

t = 1.31 s

Ahora bien, recordando los valores de tiempo hallado antes para x(t) = 3, los mismos eran

t_1 = 0.26s y t_2 = 2.37s

Respecto al primer tiempo no hay problema y es el tiempo real en el que el pingüino caería por el barranco y es cuando el pingüino se está moviendo de izquierda a derecha, respecto al segundo valor, recordemos que esa aceleración estaba causada por la fuerza de rozamiento, pero en cuanto la velocidad sea 0 (t=1.31s), esa fuerza dejará de existir y el animal permanecerá en reposo (si tuviese suficiente lugar para desplazarse y no caería al barranco) por lo que en realidad más allá que matemáticamente t=2.37s es una solución de la ecuación, en la práctica no lo es ya que nunca se desplazaría de derecha a izquierda.

Ahora sí, la solución está completa y el pingüino a los 0.26s caería al barranco por lo que se salva del cazador que tarda 4s en recargar su arma.

Salu2

¡Gracias! de bien explicado :)