Cual es el dominio e imagen de la siguiente función

Te dejo la a)

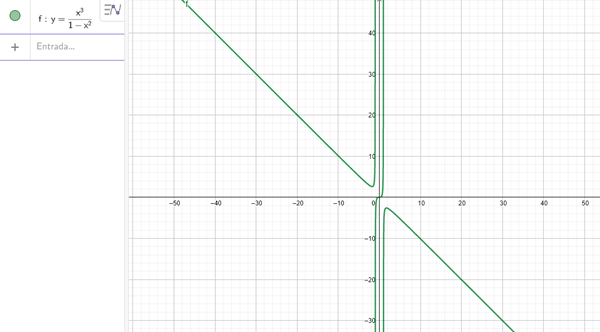
$$\begin{align}&y=\frac{x^3}{1-x^2}\\&\text{Dominio será en todos los lugares donde esté definida}\\&\text{Los polinomios son continuos en todo R, así que el único lugar en cuestión es donde}\\&\text{el denominador se hace 0}\\&1-x^2=0 \to x=\pm 1\\&Dom: R \ne \{-1, 1\}\\&\text{Para la imagen hay varias formas, yo voy a hacer x en función de y, para luego ver el dominio de esa función}\\&y=\frac{x^3}{1-x^2}\\&y(1-x^2)=x^3\\&y-yx^2=x^3\\&y=x^3+yx^2\\&\text{Acá me quedo y es bastante difícil de seguir por acá, así que voy a buscar otras alternativas}\\&\text{para buscar el rango}\\&\text{Ya sabemos donde no está definida la función, veamos que pasa en esos puntos en el límite}\\&\text{Sabemos que tenderá a infinito, el tema es si será positivo o negativo}\\&\text{Veamos a -1, por izquierda}\\&\lim_{x \to -1^-}\frac{x^3}{1-x^2} = \frac{-}{-}\to +\infty\\&\text{Veamos a -1, por derecha}\\&\lim_{x \to -1^+}\frac{x^3}{1-x^2} = \frac{-}{+}\to -\infty\\&\text{Veamos a +1, por izquierda}\\&\lim_{x \to +1^-}\frac{x^3}{1-x^2} = \frac{+}{+}\to +\infty\\&\text{Veamos a +1, por derecha}\\&\lim_{x \to +1^+}\frac{x^3}{1-x^2} = \frac{+}{-}\to -\infty\\&\text{Vemos que la función tiende a los infinitos donde no está definida, y era continua en el resto de los puntos}\\&\text{Veamos si tiene alguna asintota horizontal (para ver si hay algún valor que tal vez no alcance nunca}\\&\lim_{x \to \pm \infty}\frac{x^3}{1-x^2} \to \mp \infty\\&\text{Como no hay asintotas horizontales, el rango de la función es todo R}\end{align}$$

Veamos un gráfico para aclarar el punto

Salu2