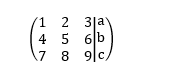Cómo resolver el Problema 3 página 25 variedades diferenciables de los apuntes de Ángel Montesinos amibilia

Pues no entiendo que es lo que tiene esa página que dices que no puedas escribir acá con la opción "Insertar fórmula matemática"

$$\begin{align}&\text{Fórmula de la cuadrática}\\&{\color{blue}a}x^2+{\color{red}b}x+{\color{green}c}=0\\&x_{1,2}=\frac{-{\color{red}b}\pm \sqrt{{\color{red}b}^2-4\cdot {\color{blue}a} \cdot {\color{green}c}}}{2\cdot {\color{blue}a}}\\&\text{Polinomio de Taylor centrado en el punto 'a'}\\&P_n(x) = \sum_{k=0}^n \frac{f^{(k)}(a)}{k!}(x-a)^k + R_n(f)\\&Donde\\&R_n(f)=\frac{f^{(n+1)}(\psi)}{(n+1)!}(x-a)^{n+1} ...(\psi \in (a,x))\\&\text{Binomio de Newton}\\&(x+y)^n=\sum_{k=0}^n {n \choose k}x^{n-k} y^k={n \choose 0}x^n + {n\choose 1} x^{n-1} y+{n\choose 2}x^{n-2}y^2 + \cdots + {n\choose n-1}xy^{n-1} + {n\choose n} y^n\\&\text{Límite}\\&\lim_{x \to a}f(x)= C\end{align}$$

Para lo que esta página es realmente muy malo es para insertar matrices, pero como bien dices, siempre puedes incluir una imagen mediante la opción "Añadir Imagen"

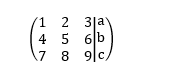
Y esas opciones que te digo te aparecen cuando estás escribiendo el texto. Al comenzar a escribir busca lo siguiente:

Salu2