Que Procedimiento debo seguir para calcular el vertice de un triangulo semejante a otro

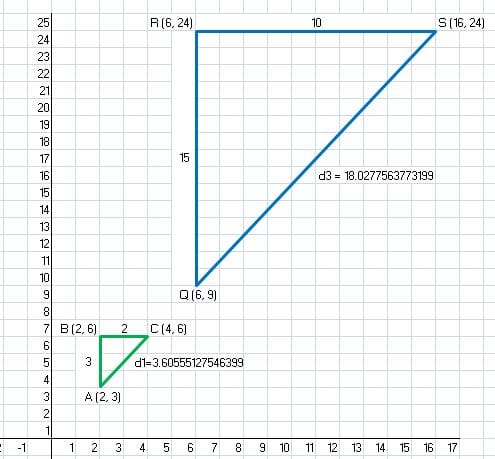
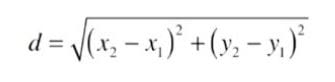Calcular el vértice S

1. Calcular distancias de cada lado de los triángulos

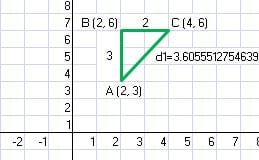
Para el triángulo ABC

distancia entre los puntos AC: A(2,3) , C(4,6)

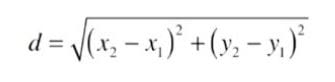
d = raíz( (x2 - x1) ^2 + (y2 - y1)^2 )
d= raíz( (4 - 2) ^2 + (6 - 3)^2 )
d= raíz( (2) ^2 + (3)^2 )
d= raíz(4 + 9)  = raíz(13)
dAB = 3.60555127546399

Te pongo ese ejemplo y ya calculas las distancias AC y BC

distancia entre los puntos AC; A(2,3) , B(4,6)

dAB = 3

distancia entre los puntos BC: B(4,6), C(4,6)

dBC = 2

Para el triángulo QRS

distancia entre los puntos QR: Q(6,9), R(6,24)

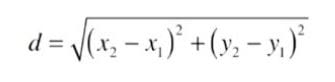
d = raíz( (x2 - x1) ^2 + (y2 - y1)^2 )
d = raíz( (6 - 6) ^2 + (24 - 9)^2 )
d = raíz( 0 + 15^2 )
d = raíz( 15^2 )
d = raíz( 225 )
d = 15

Ahora con la regla de triángulos semejantes calculamos la distancia entre R y S.

La nombramos d2

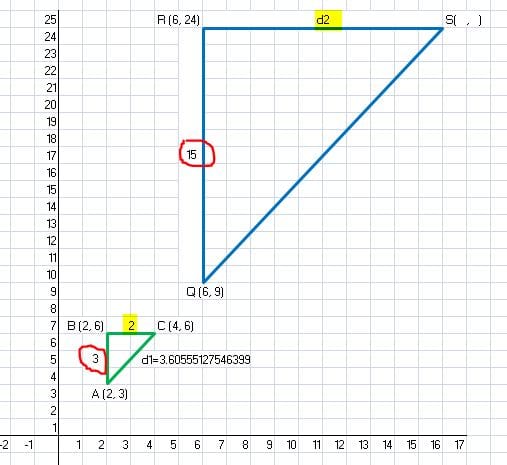
Dividimos lados iguales:

d2 / 2 = 15 / 3

Despejamos d2

d2 = ( 15 / 3 ) * 2

d2 = 5 * 2

d2 = 10

Ahora hay que calcular la distancia entre  Q y S

d3/3.60555127546399 = 15 / 3
d3 = (15 / 3) * 3.60555127546399
d3 = 18.0277563773199

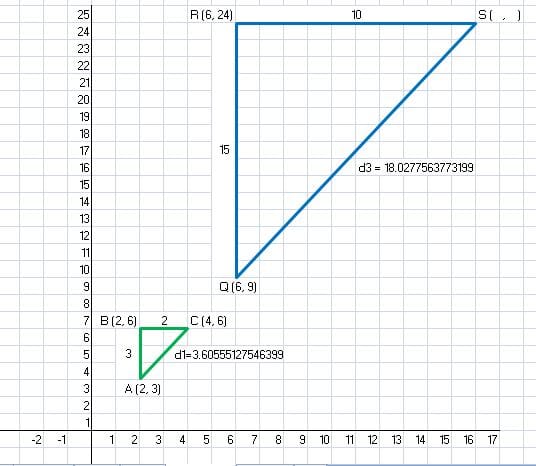
Ya tenemos todas las distancias, ahora vamos a calculas las coordenadas del vértice S

de los puntos R (6, 24) y S(  ,   ) tenemos la distancia  = 10

de la fórmula de la distancia:

d = raíz( (x2 - 6) ^2 + (y2 - 24)^2 )

10 = raíz( (x - 6) ^2 + (y - 24)^2 )               Ecuación (1)

de los puntos Q (6, 9) y S(  ,   ) tenemos la distancia  = 18.0277563773199

d = raiz( (x2 - 6) ^2 + (y2 - 9)^2 )
18.02 = raiz( (x - 6) ^2 + (y - 9)^2 )           Ecuación (2)

__________

De la ecuación (1) despejamos x:

10 = raiz( (x - 6) ^2 + (y - 24)^2 )
10^2 = (x - 6) ^2 + (y - 24)^2
10^2 - (y - 24)^2 = (x - 6) ^2
(x - 6)^2 = 10^2 - (y - 24)^2
(x - 6)^2 = 100 - (y - 24)^2                        Ecuación (3)

_________

De la ecuación (2) despejamos x:

18.02 = raiz( (x - 6) ^2 + (y - 9)^2 )
18.02^2 = (x - 6) ^2 + (y - 9)^2
(x - 6) ^2 = 18.02^2 - (y - 9)^2
(x - 6) ^2 = 325 - (y - 9)^2                         Ecuación (4)

___________

igualamos 3 y 4

(x - 6)^2 = 100 - (y - 24)^2
(x - 6)^2 = 325 - (y - 9)^2

Si te das cuenta del lado izquierdo tenemos (x - 6)^2

Entonces nos queda:

100 - (y - 24)^2 = 325 - (y - 9)^2

Despejamos y

100 - (y^2 -48y + 576) = 325 - (y^2 -18y + 81)
100 -y^2 + 48y - 576 = 325 - y^2 + 18y -81
100 -y^2 + 48y - 576 - 325 + y^2 - 18y + 81 = 0
30y -720 = 0
y = 720 / 30
y = 24                           Esta es la coordenada y para el vértice S

___________________

Sustituimos y = 24 en la ecuación (1)

10 = raiz( (x - 6) ^2 + (y - 24)^2 )

10 = raiz( (x - 6) ^2 + (24 - 24)^2 )
10^2 = (x - 6) ^2 + (0)^2
100 = (x - 6) ^2
raiz(100) = x - 6
10+6=x
x=16                   Coordenada x para el vértice S

___________________

S(16, 24)

Gráfica final: