Esto es para Matemáticos. ¿Lo pueden resolver?
¿Cómo solucionarían estas ecuaciones trigonométricas?
x - sen x = -100
x^ sen x = 20
1 Respuesta
No creo que haya una forma algebraica de hallar esas soluciones, así que voy a plantearlo por métodos iterativos, usando Newton-Raphson.
A) x - senx = -100
f(x) = x-senx + 100
f'(x)=1 -cosx
N-R plantea la iteración: x_{i+1} = x_i - f(x_i) / f'(x_i)
Como senx está entre 0 y 1, sabemos que la solución debe estar en [-100,-99], así que voy a empezar con -99.5
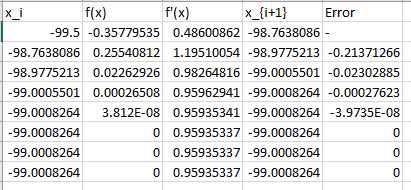
Con solo 5 iteraciones llegamos a una solución con 7 decimales, así que podemos decir que la solución es -99.0008264 (supongo que podríamos redondearlo a -99.0)
B) x^ sen x = 20
Planteamos lo mismo
f(x) = x^senx - 20
esta derivada es bastante más complicada...
f'(x) = (x^(senx) senx + x^(senx+1) cosx ln(x))/x
Que también podemos escribir como
f'(x) = x^senx / x * (senx + x cosx lnx)
Acá no está tan claro el valor por donde andará la solución, así que voy a empezar con x_0=5
En este caso se necesitaron algunas iteraciones más, pero se llegó igualmente a la solución 354.464444 que tiene 8 decimales exactos (aunque me llamó la atención, pensé que iba a encontrar una solución más baja).
Ahora sí albert, si tenés un método algebráico para encontrar estas soluciones, me gustaría conocerlo ;-)
Abrazo y buena semana!
El primer caso salio redondo.
El segundo lo estoy analizando porque tendría que dar alrededor de 20, pero tampoco encuentro manera algebraica de resolverlo.
Te informo si llego a algo.
Gracias !
Por fin me dejó contestarte Albert!
Respecto al segundo, te dejo una imagen que explica por qué pasó eso (esa ecuación tiene infinitas raíces). Yo empecé en un valor y encontré una raíz, pero usando otra semilla hubiese llegado a la raíz que vos decís (te dejo ambas imágenes).
Abrazo grande y muy entretenidos los ejercicios (lástima no tener una solución algebraica, jaja)