Problema demostración números complejos Sea α ∈ C tal que |α| < 1...
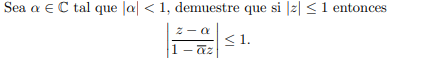
Ni idea de como proceder a la resolución, agradecida sea la ayuda.
1 Respuesta
Respuesta de Matesfacil
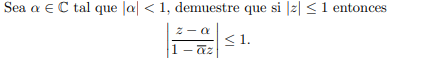
Ni idea de como proceder a la resolución, agradecida sea la ayuda.
