e)
Esta es la gráfica tridimensional, fíjate en los tres planos verticales que serán el dominio de integración y dentro estará el techo de cilindro que debemos integrar.

Respecto al dominio. Proyectados sobre el plano z= 0 los planos se trnasforman en rectas con la misma ecuación que serán:
x=0
y=0
2x+y=4 ==> y = 4 - 2x
Forman un triangulo rectángulo.
Nos hace falta el corte de esta última recta con el eje X que es:
0 = 4 - 2x ==> x = 2
Luego el dominio está bastante claro, es [0, 2] x [0, 4-2x] y la función a integrar es
f(x,y) = z = 4 - x^2
Vamos con ello como siempre.
V = $${(4-x^2) dy en y € [0, 4-2x]}dx en x €[0, 2] =
${(4-x^2)y en y € [0, 4-2x]}dx en x €[0, 2] =
${(4 - x^2)(4 - 2x)}dx en x €[0, 2] =
${16 - 8x - 4x^2 + 2x^3} en x € [0,2] =
(16x - 4x^2 - (4/3)x^3 + (1/2)x^4) en x € [0,2] =
32 - 16 - 32/3 + 8 = 24 - 32/3 = 72 -32 / 3 =
40 / 3 = 13,333...------------------------------
f) Ha habido que tomar la vista desde muy arriba para que se viera algo.

Tenemos una cónica como techo y tres planos como paredes. Luego veremos como es la proyección de estos planos sobre el eje Z para calcular el dominio de integración, dividirlo si es necesario, etc.
Las rectas que determinan el dominio son : x=1, y=x+1 , y= -x-1. Esta vez creo que conviene dibujarlas pues no se ve tan claro.
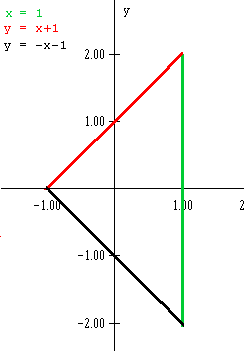
Bueno, yo pensaba que era más dificíl; pero no, no hay que dividirlo.
El dominio es [-1, 1] x [-x-1, x+1] y la funcion la consabida f(x,y) ) = z = 2x^2+y^4
V = $${(2x^2+y^4)dy en y € [-x-1, x+1]}dx en x € [-1,1] =
$ 2yx^2 + (1/5)y^5 en y = [-x-1, x+1]}dx en x € [-1,1] =
Ojo que aquí dará varios pasos en uno transformando signos
${2(x+1)x^2 + (1/5)(x+1)^5 + 2(x+1)x^2 + (1/5)(x+1)}dx en x € [-1,1] =
$ [4(x+1)x^2 + (2/5)(x+1)^5] dx en x €[-1,1] =
x^4 + (4/3)x^3 + (1/15)(x+1)^6 =
1 + 4/3 + (1/15)64 - 1 + 4/3 = 8/3 +64/15 = (24+64)/15 =
88 / 15 = 5,8666...Y eso es todo. Espero que te sirva y vayas entendiendo los problemas estos. NO olvides puntuar.



