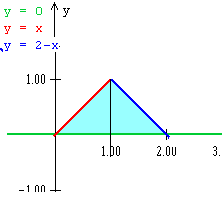Calcular el volumen (integrales)

1) Comenzaremos realizando la gráfica para estar más seguros de lo que hagamos.

El cilindro y = 1+x^2, y el plano y=5 delimitan el dominio en el plano z=0.
Pero el enunciado nos dice de hallar el área en el primer octante (que es el que tiene todos los signo positivos). En la práctica esto nos reducirá el dominio quitando la mitad de la izquierda donde la por era negativa.
Resumiendo, el dominio esta limitado por la parte derecha de la parábola, la recta x=0 y la recta y=5
En x toma valores entre 0 y 2 pues en 2 sucede y=1+2^2 =5 es el vértice que forman la parábola y la recta y=5. Cuanto lío, mejor se entenderá con un dibujo.

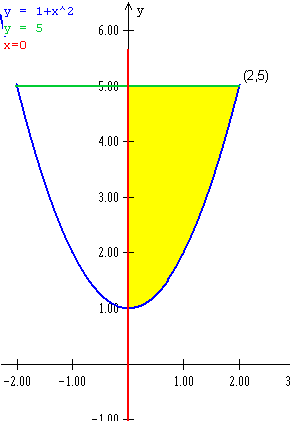
La parte amarilla es el dominio sobre el que tenemos que integrar.
Su expresión es [0,2]x[1+x^2, 5] y la función a integras es f(x,y) = z = 3x
V = $${3x dy en y € [1+x^2, 5]}dx en x € [0,2] =
${3xy en y € [1+x^2, 5]}dx en x € [0,2] =
$ 3x[5-(1+x^2)]dx en x € [0,2] =
$ (12x - 3x^3)dx en x € [0,2] =
6x^2 - (3/4)x^4 en x €[0,2] =
6·4 - (3/4)16 = 24 - 12 = 12
----------------
2) El plano z=0 hace de suelo y el palno x+y+z = 3 es el techo. Los planos y=0, y=x, x+y=2 son las paredes, sus proyecciones sobre el plano z=0 nos darán los límites del dominio de integración.
Siempre será más claro con el dibujo.

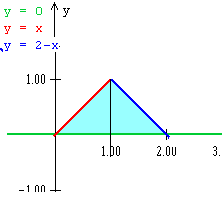
El dominio dede ser dividido en dos partes para poder expresarlo. Es
[0,1] x [0,x] U [1,2] x [0, 2-x]
La función a integrar es f(x,y = z = 3 - x - y.
Puede comprobarse que dicha función no corta al plano z=0 en el dominio, puesto que en el dominio se cumple x+y <=2 ==> z = 3 - (x+y) >= 1 con lo que la fúnción es siempre positiva y se puede integrar sin dividir en partes salvo por la culpa de la forma del dominio.
V = $${(3-x-y)dy en y€[0,x]}dx en x€[0, 1] + $${(3-x-y)dy en y€[0, 2-x]}dx en x€[1,2] =
${3y-xy-(y^2)/2 en y€[0,x]}dx en x€[0, 1]+${3y-xy-(y^2)/2 en y€[0, 2-x]}dx en x€[1,2]=
${3x - x^2 - x^2/2}dx en x€[0, 1] + ${3(2-x) -x(2-x) - (1/2)(2-x)^2}dx en x€[1,2] =
${3x - (3/2)x^2}dx en x€[0, 1] + ${6 - 3x - 2x + x^2 - 2 - (1/2)x^2 + 2x}dx en x€[1,2]=
${3x - (3/2)x^2}dx en x€[0, 1] + ${4 - 3x + (1/2)x^2}dx en x€[1,2]=
[(3/2)x^2 - (1/2)x^3] en x€[0,1] + [4x - (3/2)x^2 + (1/6)x^3] en x€[1,2] =
3/2 - 1/2 + 8 - 6 + 8/6 - 4 + 3/2 - 1/6 =
-2 + 5/2 + 7/6 = (-12 + 15 +7) / 6 = 10/6 = 5/3 = 1,666...
Y eso es todo. Espero que te sirva y lo hallas entendido. No olvides puntuar o pedir aclaraciones si no lo entendiste.