Me temo que no puede ser más fácil. El área del hexágono, volumen y superficie del prisma son fórmulas que no admiten más simplificación.
Si te resulta molesto arrastrarlo, podrías haber calculado sqrt(3) nada más que sale y llevar la expresión decimal después, quedaría así lo de después de cuando aparece por primera vez:
a = sqrt(12) = 3,4641016
Ahora
Area base = Perimetro · apotema / 2 = 6 · 4 · 3,4641016 / 2 = 41,569219 cm^2
Volumen = (Area Base) · altura = 41,569219 · 12 = 498,83063 cm^3
Superficie lateral = perimetro · altura = 24 · 12 = 288 cm^2
Superficie total = (Superficie lateral) + 2 (Area de la base) =
= 288 + 2 · 41,569219 = 288 + 83,138439 = 371,13844 cm^2
Quizá la parte más complicada sea la inicial de calcular el apotema, pero es que hay que calcularlo y hay que usar el teorema de Pitágoras por obligación, únicamente podría ayudar algo el haber hecho un dibujo.
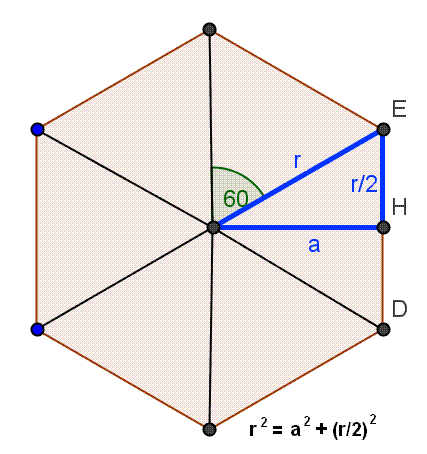
De donde se deduce visualmente que los triágulos so equiláteros y el triángulo rectángulo que crea el apotema y los elementos que hay que poner en el teorema de Pitágoras. Lo que pasa es que puse r de radio en vez de b como en el problema, pero son lo mismo.
Más no creo que pueda hacerse sin ser una clase con el profesor presente.


