Estadística matemática con aplicaciones 5.57

5.57)

Vamos a dibujar los limites de integración. Son el triángulo. Luego he dibujado dos líneas para que veas cuales son los límites de la integral de las funciones de densidad marginal.

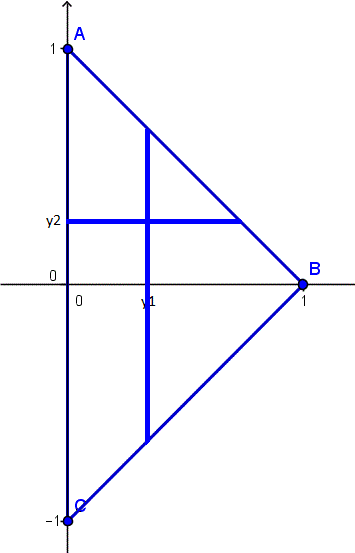
$$\begin{align}&f_1(y_1)=\int_{-1+y_1}^{1-y_1}30y_1y_2^2dy_2 =\\ &\\ &10y_1\left[y_2^3  \right]_{-1+y_1}^{1-y_1}=10y_1[(1-y_1)^3-(y_1-1)^3]=\\ &\\ &20y_1(1-y_1)^3\\ &\\ &\\ &\\ &f_2(y_2)=\int_0^{|1-y_2|}30y_1y_2^2dy_1=\\ &\\ &\\ &\\ &15y_2^2\left[ y_1^2 \right]_0^{|1-y_2|}=15y_2^2(1-y_2)^2\\ &\\ &\\ &f_1(y_1)f_2(y_2)=300y_1y_2^2(1-y_1)^3(1-y_2)^2\end{align}$$

Que es algo muy pero muy distinto de la función de densidad conjunta, luego no son independientes.

Y eso es todo.