Ejercicio 19 circulo osculador y curvatura.

Es la curva y = 1/(1+x^2) en el punto (0,1)

$$\begin{align}&f'(x) = -\frac{2x} {(1+x^2)^2}\\ &\\ &f'(0)= 0\\ &\\ &f''(x) = - \frac{2(1+x^2)^2-2x·2·(1+x^2)·2x}{(1+x^2)^2}=\\ &\\ &-\frac{2(1+x^2)-8x^2}{(1+x^2)^3}=\frac{6x^2-2}{(1+x^2)^3}\\ &\\ &f''(0)=-2\\ &\\ &K(0) = \frac{f''(0)}{\sqrt{\left[1+(f'(0))^2\right]^3}}=\frac{-2}{1}=-2\\ &\\ &\text{La ecuación paramétrica es}\\ &\\ &(x(t),y(t))=\left(t, \frac{1}{1+t^2}  \right)\\ &\\ &x'(t)=1\implies x'(0)=1\\ &y'(0)=0\quad \text{  es el f'(0) calculado antes}\\ &||f'(0)||=\sqrt{1^2+0^2}=1\\ &\\ &x''(t)= 0\implies x''(0)=0\\ &y''(0)=-2\quad \text{ tal como se calculó antes}\\ &\\ &\text{Y el centro }(x_c,y_c) \;es\\ &\\ &\left(x(0)- \frac{y'(0)}{K(0)||f'(0)||},y(0)+\frac{x'(0)}{K(0)||f'(0)||}  \right)=\\ &\\ &\left(0-\frac{0}{(-2)·1},1+\frac{1}{(-2)·1}  \right)=\left(0,\frac 12\right)\\ &\\ &\text{Y la circunferencia es}\\ &\\ &(x-x_c)^2+(y-y_c)^2=R^2\\ &\\ &\text {el radio es }R=\left|\frac{1}{K(0)}\right|=\frac 12\\ &\\ &x^2+\left(y-\frac 12\right)^2 = \frac 14\\ &\\ &\\ &\end{align}$$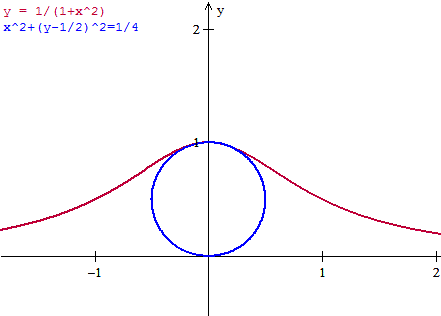

Y eso es todo.