Hallar la ecuación de la parabola

Un ejercicio como este lo dejé sin resolver por la dificultad que tenía y creo que con este puede pasar la mismo.

Se trata de resolver un sistema de tres ecuaciones dos delas cuales son cuadráticas. Si los puntos fueran simétricos sería cose y cantar pero así no lo es.

Bueno, vamos a resolverlo. Por ser el eje paralelo al eje X la variable y es la que estará al cuadrado.

(y-b)^2 =2p(x-a)

por pasar por esos puntos

(5-b)^2 = 2p(3-a) ==> 2p = (5-b)^2 / (3-a)

(-1-b)^2 = 2p(6-a) ==> 2p = (1+b)^2 / (6-a)

luego igualando

(5-b)^2 / (3-a) = (1+b)^2 / (6-a)

(6-a)(5-b)^2 = (3-a)(1+b)^2

Y el punto (a,b) pasa por la recta luego cumple

b = 6a+12 ==>

a = b/6 - 2

sustituyendo a en la anterior

(6 - b/6 + 2)(5-b)^2 = (3 - b/6 + 2)(1+b)^2

(8-b/6) (25 + b^2 - 10b) = (5-b/6) (1+b^2+2b)

200 + 8b^2 -80b - (25/6)b - (1/6)b^3 + (5/3)b^2 = 5 + 5b^2 +10b - b/6 - (b^3)/6 - (b^2)/3

5b^2 + b(-80 - 25/6 -10 + 1/6) +195 = 0

5b^2 - 94b + 195 = 0

b = [94 +-sqrt(8836 - 3900)]/10 =

[94 +- sqrt(4936)]/10 =

[47 +- sqrt(1234)]/5

Ahora calculamos a de acuerdo con a = b/6 -2

a = [47 +- sqrt(1234)]/30 - 2 = [-13 +- sqrt(1234)]/30

Esto pasa por no estar bien preparado el problema. Es una heroicidad seguir trabajando con las expresiones exactas, si queremos terminar el problema voy a tomar la calculadora y calcular con números decimales

b = 16.425667 y 2.3743328

a = 0.7376112 y -1.6042779

Y ahora calculamos 2p

2p = (5-b)^2 / (3-a) = 57.702666 y 1.497331

Y las parábolas posibles, porque son dos, son estas

(y-16.425667)^2 = 57.702666(x-0.7376112)

(y-2.3743328)^2 = 1.497331(x+1.6042779)

Y como no estaba muy seguro he hecho la gráfica y están bien.

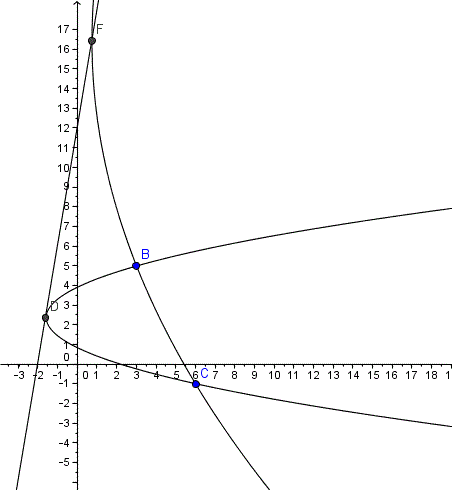
Realmente me parece una pasada este ejercicio a comparación de los otros. O es un inconsciente el que lo ha escrito o hay algo que está mal escrito o hay un método revolucionario para resolverlo que yo desconozca. NO haré ninguno más de este estilo.

Y eso es todo.