Razón de cambio y tangentes de una curva
Dada la función f(x)=x^2-2x, hallar la ecuación de la recta tangente a dicha función que es papralela a la recta normal que pasa por el punto (3,3)
1 Respuesta
La ecuación de la recta normal en un punto (xo,yo) es
y = yo - [1/f(xo)](x-xo)
Aunque para lo que nos piden solo nos interesa la pendiente de la recta normal que es
p= -1/f(xo)
En este ejercicio
f '(x) = 2x-2
f '(3) = 6-2 = 4
p = -1 / f' (3) = -1/4
Una
recta paralela a esta tendrá la misma pendiente, luego su derivada será
-1/4. Ya que la pendiente de la recta tangente es la derivada en el
punto de tangencia.
f '(xo) = -1/4
2xo-2 = -1/4
2xo = -1/4 +2
2xo = 7/4
xo = 7/8
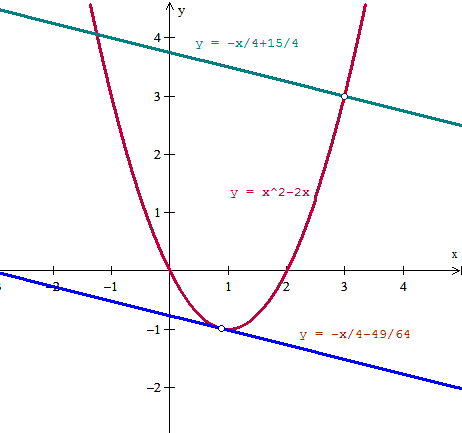
yo = (7/8)^2 - 2(7/8) = 49/64 - 14/8 = (49-112)/64 = -63/64
El punto es (7/8 , -63/64)
Y la recta tangente en él es:
y = -63/64 - (1/4)(x-7/8)
y = -63/64 - x/4 + 7/32
y = -x/4 - 49/64
Aquí está la gráfica que he hecho para verificar si está bien:
Y eso es todo.
