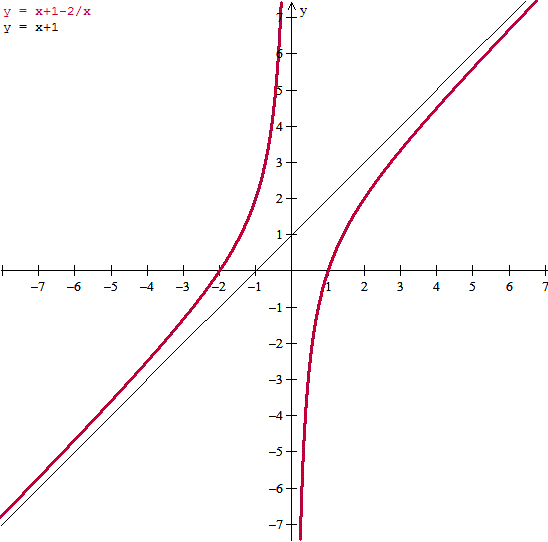Ejercicio de funciones
Hola buenas noches experto me dirijo a usted para si que le eche un vistazo a este ejercicio que no sé si está bien o no.
Considera la función f definida, para x pertenece a R, X no es igual a 0, por
$$f(x) =x +1 - \frac{2}{x}$$A. Hallar los puntos de corte de su gráfica con los ejes de coordenadas.
B. Halla las asíntotas de su gráfica.
C. Calcula sus máximos y mínimos relativos (valores y dónde se alcanzan) y justifica en qué intervalos es creciente o decreciente.
D. Esboza la gráfica de f.
Con el eje OX tengo de puntos de corte : (1,0) y ( -2,0).
Con el eje OY :
$$- \infty$$
Asíntotas verticales me da - infinito
No hay asíntotas horizontales
Asíntotas oblicuas me da : y= x+1
No me da máximos ni mínimos.
Es creciente en todo R menos en 0 porque anula el denominador.
Muchas gracias por su ayuda.Saludos
1 respuesta
Vamos a comprobarlo
f(1) = 1 + 1 - 2/1 = 0
f(-2) = -2 + 1 -(-2)/2 = -2 + 1 +1 = 0
Estos están bien.
Con el el eje Y no puede haber corte ya que la función no está definida en x=0.
No obstante se puede calcular el límite para ver a dónde tiende la función
lim x-->0 de (x+1-1/x) = +- oo
Por la izquierda tiende a +oo y por la derecha a -oo
La asíntota es una recta. La vertical es la recta x=a donde el límite de la función en a es infinito.
Ya hemos visto que el límite en cero es infinito, luego la recta vertical que pasa por el cero es la recta
r: x=0
Esa es la asíntota vertical. Puede haber varias, pero en esta función solo existe esa.
Las asíntotas horizontales son los límites de la función en +- infinito si existen y son finitos. No existen porque ese límite es +- infinito
Las asíntotas oblicuas tienen por pendientes m los limites de la función dividida por x si son finitos y distintos de cero
m = lim x-->oo (x+1-2/x) / x = lim x-->oo (1 + 1/x - 2/x^2) = 1
hay una asíntota oblicua de pendiente 1.
Y el valor b de la recta y=mx+b se calcula como
lim x-->oo (f(x)-mx) =
lim x-->oo (x + 1- 2/x - 1x) =
lim x-->oo (1 - 2/x) = 1
Luego la asíntota oblicua tiene ecuación
y=x+1
Para los máximos y mínimos relativos derivamos e igualamos a cero
f'(x) = 1 + 1/x^2 = 0
No los hay porque eso es siempre positivo
Y como es siempre positivo la función es siempre creciente. En x=0 nada porque no está definida la función.
Y la gráfica es esta:
Y eso es todo.
Hola experto lo he entendido todo pero referente a los máximos y mínimos yo he hecho:
$$\begin{align}&y=x+1-\frac{2}{x} \\ &\\ &y´=1+\frac{2}{x^2}\end{align}$$Igualo a cero la derivada y me da x^2+2=0 de donde : x= + - raíz cuadrada de -2, por lo tanto no tiene solución y no esta incluido en los números reales.
Y como el 2 anula el denominador de la fracción original entonces no lo he incluido en la solución final diciendo que crece en toda la función menos en el punto 0.
Es correcto.
Gracias y saludos
Si, se me olvido el 2 de la derivada y la derivada es la que te sale a ti
y' = 1+2/x^2
que igualada a cero es
1+2/x^2 = 0
x^2 + 2 = 0
x^2 = -2
Y no hay soluciones reales, luego la derivada no se anula nunca y como es siempre positiva la función sera creciente en todos los puntos donde sea derivable.
El cero no pertenece al dominio de la función, no hay que hablar de él, simplemente hay que decir que la función es creciente en todo su dominio.
Eso es todo.
