Solución ejercicio 9 pagina 337
Puedes ayudarme por favor con el ejercicio 9 de la siguiente imagen:
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1
1 <= x^2 +y^2 <= 2
1 - x^2 <= y^2 <= 2-x^2
se deducen dos
y^2+x^2>=1
y^2+x^2<=2
La primera representa el exterior de un círculo de radio 1, la segunda el interior de un círculo de radio raíz de 2. Esto es una corona circular. Como y>=0 es la mitad superior de una corona circular.
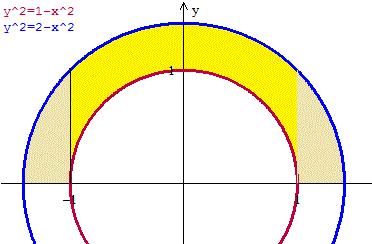
Pues en la página 332 comenta, pero no dice exactamente lo quien es una región elemental, luego mal se puede contestar la pregunta.
La región es y-simple pero no es x-simple. Si eso es una región elemental lo será, yo no lo Para hacer la integral he dividido el dominio en tres trozos tal como se ve.
$$\begin{align}&\iint_D (1+xy)dA=\\ &\\ &\\ &\int_{-\sqrt 2}^{-1}\int_0^{\sqrt{2-x^2}}(1+xy)dydx+\\ &\\ &\\ &\int_{-1}^1\int_{\sqrt{1-x^2}}^{\sqrt{2-x^2}}(1+xy)dydx+\\ &\\ &\\ &\int_1^{\sqrt 2}\int_0^{\sqrt{2-x^2}}(1+xy)dydx=\\ &\end{align}$$No es tan sencilla de hacer, ahora no puedo.
