Estadística matemática con aplicaciones m

4.17)

a) La integral entre -oo y + oo de la función de densidad es lo mismo que la integral entre 0 y 1.

$(cy^2 + y) dy en [0, 1]= c(y^3)/3 + (y^2)/2 en [0, 1] = c/3 + 1/2

Y ese cantidad debe ser 1, luego

c/3 + 1/2 = 1

c/3 = 1/2

c = 3/2

b) La función de densidad definitiva es

(3/2)y^2 + y en [0,1] y 0 en el resto

y la integral es

(y^3)/2 + (y^2)/2 + C

Como para 0 debe valer 0

C=0

F(y) =

0 si y € (-oo, 0)

(y^3)/2 + (y^2)/2 si y € [0,1]

1 si y € (1, +oo)

c)

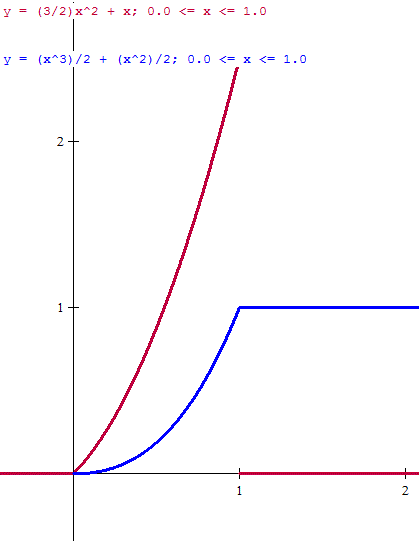
En marrón la de densidad y en azul la de distribución.

d)

F(-1) = 0

F(0) = 0

F(1) = (1^3)/2 + (1^2)/2 = 1/2 + 1/2 = 1

e) Eso será la función de distribución en 0,5 horas

F(0,5) = (0,5^3)/2 + (0,5^2)/2 = (0,125 + 0,25)/2 = 0,375/2 = 0,1875

f)15 minutos es la cuarta parte = 0,25 horas

Es la probabilidad condicionada P (Y >= 0,5 | Y >= 0,25)

La intersección de los dos intervalos es Y>=0,5 luego por la fórmula de la probabilidad condicionada

P (Y >= 0,5 | Y >= 0,25) = P( Y >= 0,5) / P(Y >= 0,25) =

[1 - P(0,5 >= Y)] / [1 - P(0,25 >= Y)] =

[1 - F(0,5)] / [1 - F(0,25)] =

La primera F ya estaba calculada

(1 - 0,1875) / [1 - (0,25^3)/2 - (0,25^2)/2] =

0,8125 / (1- 0.007825 - 0.03125) =

0,8125 / 0,9609925 = 0,84548

Y eso es todo.