Área limitada por funciones
Tengo el siguiente ejercicio:
Las rectas y curvas son las de la siguiente imagen y el área que me preguntan a mi entender es la que he sombreado.
[url=http://s3.subirimagenes.com:81/privadas/previo/thump_18343298.jpg]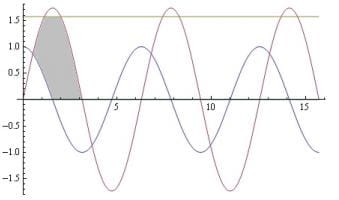
[/url]
Yo solamente se resolver ejercicios de áreas si están limitadas solamente por 2 funciones y sus correspondientes intervalos de integración.
Pero aquí el área me la limitan a la vez las 4 funciones. Me imagino que después de sacar puntos de corte la única forma sera plantear como una integral doble.
También había pensado plantear una integral con un área que pueda definir y a partir de ella ir restándole las integrales con las áreas según pueda ir definiendolas.
Como se resolvería?
Gracias anticipadas.
1 Respuesta
Ahora no tengo tiempo, dentro de unas horas si. Pues de las dos formas que dices se puede hacer, sumando los trozos que están dentro o calculando alguno que englobe lo de dentro y restando lo que sobre. Es importante que observes bien el dibujo, hazlo más grande si es necesario y nadie te va a librar de calcular los puntos de corte, eso si.
Dentro de esas horas que te digo me pongo con ello si lo sigues necesitando.
El punto de intersección
y = cosx
y = sqrt(3)·senx
es
cos^2(x) = 3sen^2(x)
1-sen^2(x) = 3sen^2(x)
1= 4sen^2(x)
sen^2(x) = 1/4
senx = 1/2
x = Pi/6
Luego es el punto (Pi/6, sqrt(3)/2)
El punto de intersección de Y = cosx con eje X es (Pi/2, 0)
El punto de intersección de y=sqrt(3)senx con el eje X es (Pi, 0)
Los puntos de corte de y = sqrt(3)senx con y = PI son
UN MOMENTO. O has hecho mal el dibujo o enunciado es incorrecto, la recta del dibujo es la recta y = Pi, mientras que el enunciado dice la recta x=Pi. Es algo distinto, la del enunciado sería vertical.
Confírmame con que versión me quedo. Yo creo que con la de la recta x=Pi, la figura sería como una especie de mariposa con un ala más grande.
