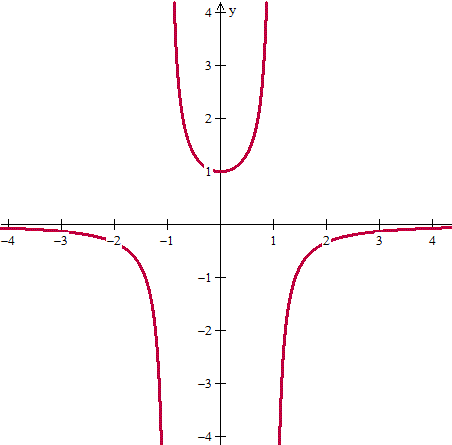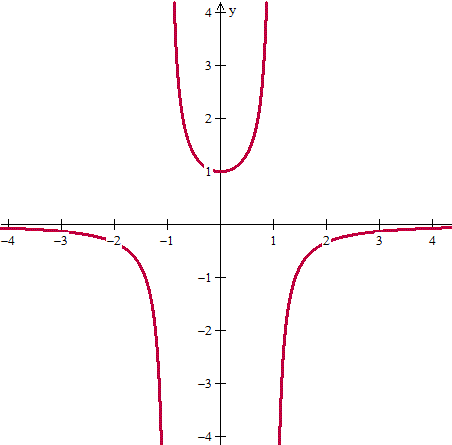Extremos relativos, punto de inflexión e intervalos de concavidad y convexidad de 1/(1-x^2)

a) Es una función de simetría par que son las que cumplen f(-x) = f(x) ya que

f(-x) = 1/[1-(-x)^2] = 1/(1-x^2) = f(x)

b) La función es continua salvo en los puntos donde se anula el denominador.

1-x^2 = 0

x^2 = 1

x = -1 y 1

F es continua en el conjunto R - {-1, 1} y es discontinua en el conjunto {-1, 1}

El límite tanto en -1 como 1 es -oo por un lateral y +oo por el otro, son discontinuidades inevitables (o de primera especie) de salto infinito.

c) Las derivadas son

$$\begin{align}&f'(x) = \frac{2x}{(1-x^2)^2}\\ &\\ &\\ &f''(x)= \frac{2(1-x^2)^2-2x·2(1-x^2)(-2x)}{(1-x^2)^4}=\\ &\\ &\\ &\frac{2-2x^2+8x^2}{(1-x^2)^3}=\frac{6x^2+2}{(1-x^2)^3}\end{align}$$

La derivada primera solo se anula en x=0

Y el valor de la derivada segunda en x=0 es 2/1 = 2 que es positivo.

Luego en x=0 hay un mínimo relativo. Su valor es f(0) = 1/(1-0^2) = 1

Es decir, el mínimo relativo es el punto (0, 1)

Puntos de inflexión no hay ya que el único que podría ser ha resultado ser un mínimo

La concavidad hacia arriba (forma de U) es cuando la derivada segunda es positiva y la concavidad hacia abajo es cuando la derivada segunda es negativa. Hace ya tiempos que dejé de usar las palabras concavidad y convexidad porque cada libro decía cosas distintas sobre cuál era cada una.

La derivada segunda no se anula nunca, pero como es discontinua puede presentar signos distintos en los intervalos determinados por los puntos de discontinuidad. Estos puntos de discontinuidad son -1 y 1

En el intervalo (-oo, -1) la derivada segunda es negativa como se puede comprobar tomando el punto -2 por ejemplo:

f ''(-2) = [6(-2)^2 +2] / [1-(-2)^2]^3 = 26 / (-27) = -26/27

Luego la función es cóncava hacia abajo en (-oo, -1)

En el intervalo (-1,1) la derivada es positiva, lo comprobamos en x=0

f ''(0) = 2/1 = 2

Luego la función es cóncava hacia arriba en (-1,1)

Y en el intervalo (1, oo) la derivada segunda negativa

f''(2) = (6·2^2 +2) /(1-2^2)^3 = 26/(-27) = -26/27

Luego la función es cóncava hacia abajo en el intervalo (1, oo)

Y la gráfica es esta: