Calculo tangente de una curva
HAllar las ecuaciones de las rectas tangentes a la función f(x)=(x-1)/(x+1) que sean que formen un angulo de pi/4 con respecto a la horizontal
1 Respuesta
La derivada es la tangente trigonométrica del ángulo que forma la recta tangente con el semieje OX+. Luego esas rectas tangentes formarán Pi/4 = 45º y la tg(45º)=1
Por lo tanto serán rectas tangentes en puntos donde la derivada valga 1. Vamos a calcular cuáles on esos puntos
f '(x) = [x+1-(x-1)] / (x+1)^2 = 2/(x+1)^2
2/(x+1)^2 = 1
2 =(x+1)^2
x+1= +- sqrt(2)
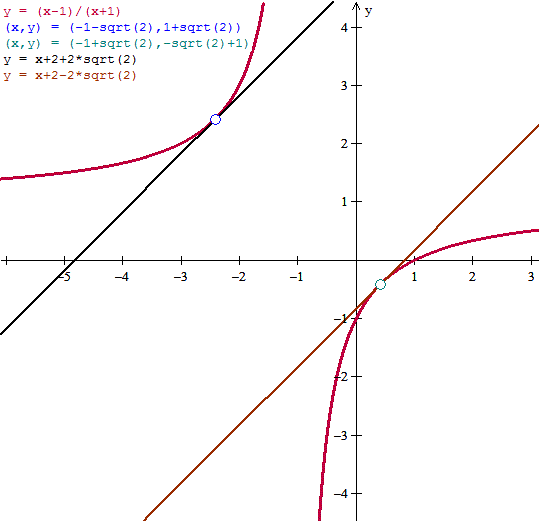
x1= -1 - sqrt(2)
x2 = -1 + sqrt(2)
ahora hallamos las coordenadas y de los puntos
y1 = - [2+sqrt(2)]/-sqrt(2) = sqrt(2)+1
y2 = [-2+sqrt(2)]/sqrt(2) = -sqrt(2)+1
Y ahora usamos la fórmula de la tangente en el punto (xo,yo)
y = yo + f '(xo)(x-xo)
La recta primera es
r1: y = 1+sqrt(2) + 1[x-(-1-sqrt(2))]
y = x +2 +2sqrt(2)
r2: y = 1 - sqrt(2) + 1[x-(-1+sqrt(2))]
y = x + 2 - 2sqrt(2)
Esta es la gráfica para confirmar los resultados obtenidos.
Y eso es todo.
