Aplicación de la derivada 4

Es un polinomio, está definida en todo R, es continua, derivable y no tiene asíntotas, como todos los polinomios.
Podemos calcular las intersecciones con los ejes.
Para los cortes con el eje X hay que resolver
x^3 - 3x - 2 = 0
Probamos a ver si hay una solución entera, sería 1, -1, 2 o -2. Se comprueba que -1 lo es
(-1)^3 - 3·(-1) - 2 = -1 + 3 - 2= 0
dividimos por Ruffini

    1   0  -3  -2
-1     -1   1   2
    -------------
    1  -1  -2  |0
-1     -1   2
    ----------
    1  -2  |0

f(x) = (x+1)(x+1)(x-2)

Luego las intersecciones con el eje Y son -1 y 2
El -1 es raíz doble, no se si te habrán enseñado que eso significa que la función es tangente al eje X en -1.
Y el corte con en eje Y es y=-2.

Y vamos ya con las aplicaciones de la derivada. Calculamos las derivada primera
f(x) = x^3 - 3x - 2
f '(x) = 3x^2 - 3
Veamos las raíces de la derivada
3x^2 - 3 = 0
3x^2 = 3
x^2 = 1
x = +- 1
En el intervalo
(-oo, -1) calculamos f '(-2) = 12-3 = 9 >0 luego la función crece
(-1, 1) calculamos f '(0) = -3 <= luego la función decrece
(1, +oo) calculamos f '(2) = 12-3 = 9 >0 luego la función crece
La derivada segunda es
f ''(x) = 6x
f ''(-1) = -6 <0 luego x=-1 es máximo relativo
f ''(1) = 6 > 0 luego x=1 es mínimo relativo
los puntos concretos son
máximo relativo (-1 , (-1)^3 -3(-1)-2)) = (-1, 0)
mínimo relativo (1 , 1^3 -3·1 - 2) = (1, -4)
Y también podemos calcular la concavidad
f ''(x) = 6x
Si x<0 la derivada segunda es negativa luego es cóncava hacia abajo
Si x>0 la derivada segunda es positiva luego es cóncava hacia arriba

Y con esos datos y algún punto extra si se quiere calcular, tendremos la gráfica.

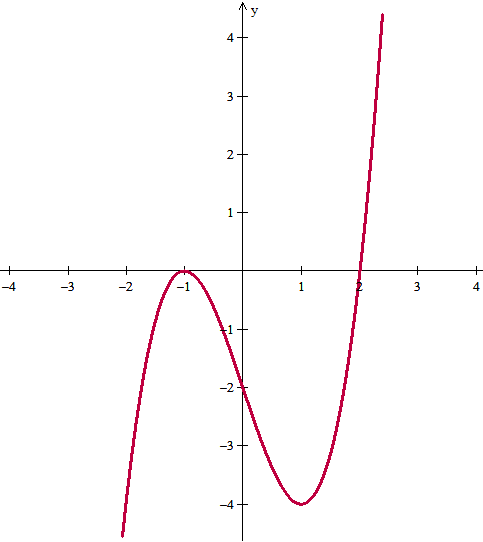
Y eso es todo.