Hola ! Me ayudan ? Dada la función ...Y= 5x
dada la función y =
$$(5x^3 + 5x^2 -2ox-20)/(5x+5)$$
a) Clasificarla de acuerdo a las operaciones que afectan a la variable independiente. Justificar.
b) Graficar . Indicar dominio y conjunto imagen.
c)¿Admite inversa? Justificar
No entiendo que quiere decir
"Clasificarla de acuerdo a las operaciones que afectan a la variable independiente. justificar".
¿A qué clasificación nos referimos? Lineal, cuadrática, cúbica, cuártica, racional. Continua o discontinua y si es discontinua evitable o inevitable. O es otro tipo de clasificación. Muchos problemas no se entienden si no se conoce el contexto donde aparecen en el libro. Y ese solo me lo puedes decir tú.
eso es lo que no entiendo, asi esta escrito por eso mi pregunta. Saludos!!
a)
Pues es que eso solo podría saberlo yendo a tu curso o con tu libro.
Espera que me parece que he encontrado un libro que viene como anillo al dedo.
Primeramente es una función escalar por ser de R en R.
Segundo es una función algebraica porque las operaciones están entre estas: suma, resta, producto, cociente potencia y raíz.
Y dentro de las algebraicas es racional porque la variable no se somete a radicación.
Y aún más, es fraccionaria por ser cociente de polinomios, si no hubiera cociente sería entera.
Luego es una función escalar, algebraica, racional y fraccionaria.
Aquí está el enlace al libro
No conocía yo la clasificación con tanto detalle, yo simplemente la hubiera definido como racional o como cociente de polinomios.
b)
Esta es la gráfica.
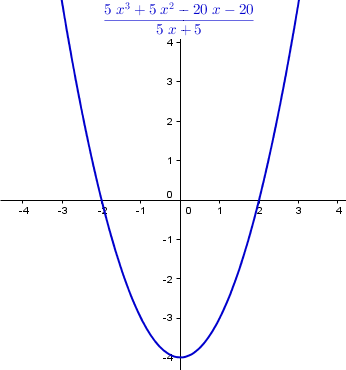
El dominio son todos los puntos salvo los que anulan el denominador
5x+5=0
5x=-5
x=-1
Dom f = R - {-1}
Para la obtención de la imagen hay que factorizar el numerador porque vamos a ver que se simplifica la función. En efecto, el denominador es 5(x+1), veamos que el numerador también tiene el factor (x+1). Tendrá ese factor si -1 es raíz del numerador
5(-1)^3 + 5(-1)^2 - 20(-1) - 20 = -5+5+20-20 = 0
Luego -1 es raíz del numerador, vamos a dividirlo por Ruffini
5 5 -20 -20
-1 -5 0 20
------------------
5 0 -20 0luego tenemos
y = (x+1)(5x^2 - 20) / [5(x+1)] = (5x^2-20)/5 = x^2 - 4
Y de y=x^2-4 podemos ver que el menor valor que toma es -4 y su límite en infinito es infinito. Como es continua toma todos los valores intermedios, luego
Im f = (-4, +infinito)
c) No admite inversa en todo el dominio porque no es una función inyectiva pero soi tomamos un intervalo del dominio donde sea inyectiva si tiene inversa.
Por ejemplo, si tomamos
f(x): [0, oo) -------> (-4, oo)
si admite inversa que se calcula así
y = x^2-4
y-4 = x^2
x = ¿+-? sqrt(y+4)
f-1(x) = ¿+-? sqrt(y+4)
Para saber cual de los dos signos tomar tengamos en cuenta que cuando x tiende a +infinito y tiende a +infinito en f, luego la inversa de +infinito debe ser +infinito, para ello debe ser el signo +
f-1(x) = sqrt(y-4)
Bueno, a lo mejor este razonamiento no te ha gustado, entonces toma un valor cualquiera distinto de 0
por ejemplo x=3
f(3) = 3^2-4 = 5
Ahora debe cumplirse
f-1(5) = 3
¿+-? sqrt(5+4)=3
luego el signo debe ser el + y la inversa es
f-1(x) = sqrt(y-4)
No pienses que la elección del signo es algo intranscendente, alguna vez la inversa corresponde al signo menos.
Y eso es todo.
