Necesito ayuda para resolver un problema de análisis matematico
el problema de integrales dobles dice así:
calcule el área de la región limitada por las curvas:
x^2 - 2 xy + y^2 + x + y = 0
x + y + 4 = 0
(Leer bien la primera curva. Asociativa y una adecuada sustitución)
1 respuesta
En un problema de este tipo es necesario hacer la gráfica para poder hacer algo.
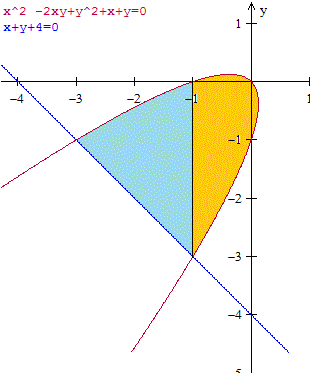
Como el corrector ortográfico no puede ver las equis sueltas habrá que usar zeta en su lugar, será más incomprensible pero no nos dejan otro remedio
Vemos que el área es la suma de la de dos figuras.
La izquierda esta limitada por la rama superior de la función en rojo y la recta de la función en azul. La derecha esta limitada por las ramas superior e inferior de la función en rojo.
Respecto a los límites en el eje EQUIS son -3 y -1 para la figura izquierda y los limites de la figura derecha son -1 y algo más difícil de comprobar que ahora vamos a calcular.
Como te decía, las equis son zetas:
z^2 - 2zy + y^2 + z + y = 0
y^2 + (1-2z)y + z^2 +z = 0
y = [(2z-1) +- sqrt((1-2z)^2 - 4(z+z^2))] / 2
y = [(2z-1) +- sqrt(1+4z^2 - 4z - 4z - 4z^2)] / 2
y = [(2z-1) +- sqrt(1-8z)] / 2
La que llamaba rama superior es la función
f(z) = [(2z-1) + sqrt(1-8z)]/2
Y la inferior
f(z) = [(2z-1) - sqrt(1-8z)]/2
Ambas coinciden en ese punto más a la derecha que es el máximo z para el que están definidas. Es decir, cuando 1-8z pasa a ser negativo
1-8z=0
z =1/8
Luego el límite derecho de integración de la figura de la derecha es 1/8-
El problema consiste calcular las áreas de las dos figuras. Para ello hay que hacer las integrales dobles de la función identidad entre los límites que te he dicho.
Y aquí paro para preguntarte si sabrías seguir tu. Si no, dímelo y continuaré la resolución, pero ahora tengo que ir a hacer otras cosas.
mirándolo bien interprete ya tu resolución ....aplicaste la ecuación de la resolvente para sacar el valor de la función roja.....y interprete que las letras sqrt es la raíz cuadrada...jajaa...
gracias ahora si ya puesdo resolver la integral
Era la suma de estas dos integrales:
$$dydz con limites en y de [-z-4, (2z-1+sqrt(1-8z))/2] y en z de [-3,-1]
$$dydz con límites en y de [(2z-1-sqrt(1-8z))/2, (2z-1+sqrt(1-8z))/2] y en z de [-1, 1/8]
No tiene mucha dificultad, simplemente cuando tengas que integrar sqrt(1-8z) lo pones como (1-8z)^(1/2) ves que la integral es -(1/8)(2/3)(1-8z)^(3/2)=-(1/12)(1-8z)^(3/2)
Te doy la respuesta calculada con Derive para que veas si lo hiciste bien:
37/12 + 9/4 = 64/12 = 16/3
Sqrt(z) es la forma internacional de expresar la función raíz cuadrada. En cualquier lenguaje de programación y aplicación gráfica o de cálculo (que no esté traducida al español como Excel por ejemplo) tendrás que usar sqrt.
Y eso es todo. No olvides puntuar
