Dada la función f(por) halla el área limitada por la curva y=f(por), el eje OX y la recta x=e

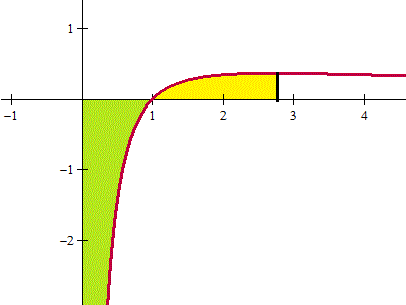
Esta función solo está definida para valores positivos de x. Entonces cambia de signo donde cambia el logaritmo neperiano que es en x=1. Antes de x=1 es negativa y después positiva. No tengo claro si quieren el área entre [0, 1] y [1, e] o solamente la de [1,e], el lenguaje no es claro.

De todas formas hagamos la integral indefinida y luego hacemos lo que queramos

$$\begin{align}&\int \frac{lnx}{x}dx =\\ &\\ &t=lnx  \quad\quad dt =\frac{dx}{x}\\ &\\ &\\ &= \int tdt = \frac{t^2}{2} = \frac{(lnx)^2}{2}\\ &\\ &\text{Si fuese en [1, e]}=\frac 12-0=\frac 12\end{align}$$

Y eso debe ser, porque en [0,1] el área es infinita ya que el límite cuando x tiende a cero del logaritmo es -infinito.

Luego el área es 1/2.

Y eso es todo.

creo que en la gráfica hay un área entre la curva de y=f(x), el eje de coordenadas (x,0) y una recta x=e, esa área esta limitada... es casi igual al ejercicio del eje OY