Problema optimización 3 para valeroasm
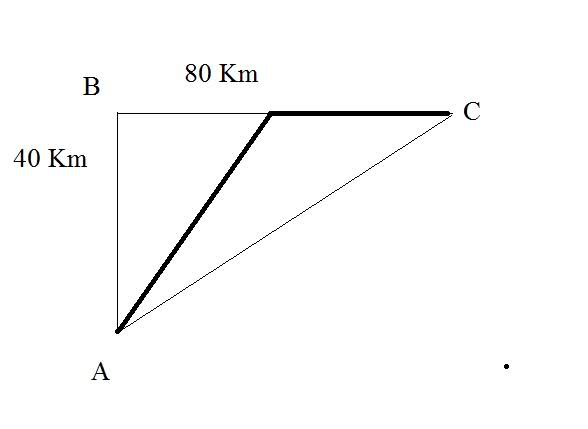
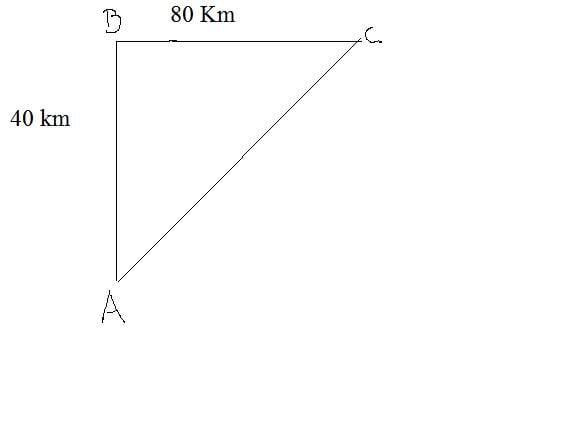
A, B y C son tres pueblos, ¿Dónde tengo que poner el corte para que la autovía sea lo más barata posible? Debemos de tener en cuenta que 50000 euros cuesta del tramo A y B. Y del trabo B al C cuesta 40000 euros.
1 respuesta
A ver, es por dónde tiene que cortar la línea que va de A-C, para que pase por B-C y así los gastos de la autovía sea mínimos, teniendo en cuenta que construir la autovía que va del tramo A y B cuesta 50000 euros y la que va del tramo B al C cuesta 40000 euros.
¿Me he explicado bien? :$
No, no me he enterado de nada.
Dime la trayectoria de la autovía. Aun mejor si la dibujas.
Y dime si el coste ese es por cada kilómetro o por el total de los kilómetros.
A ver si lo entiendes ya T_____T Lo de la línea más gruesa es lo que tiene que hacer la autovía, entonces tenemos que averiguar en qué kilómetro exactamente tiene que cortar en ese tramo para que los gastos sean mínimos a la hora de hacer la autovía. El tramo A y B cuesta 50000 euros/Km y el tramo B-C cuesta 40000 euros/ Km
¡Acabose!
Entonces el pueblo B se queda sin autovía. Es que era un enunciado incomprensible. Bueno, voy a resolver esto último que has dicho.
Sea d la distancia de B al punto de corte
Los km de autovía a 40000€ serán 80-d
Los km de autovía a 50000€ serán por el teorema de Pitágoras
sqrt(40^2+d^2)
El precio será
P(d) = 40000(80-d)+50000sqrt(40^2+d^2)
Derivamos respecto de d e igualamos a 0
P'(d) = -40000 + 50000d/sqrt(40^2+d^2) = 0
50000d/sqrt(40^2+d^2) = 40000
50000d = 40000sqrt(40^2+d^2)
5d = 4 sqrt(40^2+d^2)
25d^2 = 16(40^2+d^2)
25d^2 = 16·40^2 + 16d^2
9d^2 = 16·40^2
Extraemos la raíz cuadrada en los dos lados
3d = 4· 40
d = 160/3 = 53.3333... km
Y esa es la distancia del punto B al punto de corte.
