Pregunta de calculo h
agradezco su ayuda en estos ejercicios ya que son de puro razonamiento y no los entiendo
Tomemos un ejemplo bien sencillo
f : R ---> R
f(x) = x^2
no es lineal porque
f(x+y) = (x+y)^2 = x^2 + y^2 + 2xy
lo cual es distinto de
f(x)+f(y) = x^2 + y^2
Siempre que x y y sean distintos de 0
El efecto deja la misma coordenada x de los puntos pero les cambia la coordenada y a los puntos donde y es distinto de cero.
Luego será una transformación
(x, y) -----> (x , f(x,y))
Oye, esto no es tan sencillo. ¿Podrías decirme el libro donde sale.?
Eso es un taller pero trabajams de libro de Álgebra de Grosman
¿Pero sale el ejercicio en ese libro? Y si no dime cuanto menos las páginas correspondientes a la teoría de este ejercicio.
pues es de la parte del álgebra lineal de la grosman de la sección de transformaciones lineales capitulo 4 pero ahi no esta el ejercicio
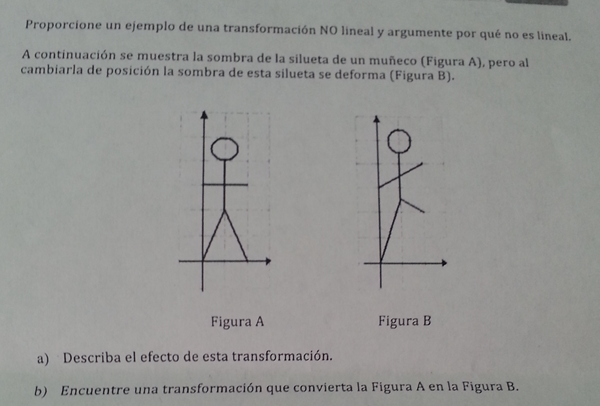
Es que la pierna derecha lo fastidia todo. Si en vez de estar la punta del pie derecho en (2,2) estuviera en (2,1) sería un corte a lo largo del eje Y, tal como lo tienes en la página 490-491
f(x, y) = (x, y + cx)
que en ese caso sería c=2 ya que para x=2 se sube 1 en el eje y
f(x, y) = (x , y + x/2)
Esa sería la transformación.
Pero tal como está el dibujo es muy probable que se hayan confundido y no haya transformación lineal que lleve una figura a la otra. Cuando dejé el ejercicio es porque era bastante difícil o imposible.
Estas son algunas transformaciones
f(0,3) = (0,3)
Supongamos que existe una matriz que representa esa transformación lineal
(a b) x (0) = (0a+3b)
(c d) (3) (0c+3d)
luego
3b=0 ==> b= 0
3d=3 ==> d =1
ahora debe cumplir
f(2,0) = (2,2)
(a 0) x (2) = (2a)
(c 1) (0) (2c)
luego
2a = 2 ==> a=1
2c = 2 ==> c=1
Luego la matriz sería
(1 0)
(1,1)
Pero esta matriz no cumple
f(2,3) = (2,4)
ya que
(1 0) x (2) = (2) = (2)
(1 1) (3) (2+3) (5)
Luego o se han equivocado en el dibujo o es una transformación no lineal del plano.
Y eso es todo.
