Calcula el área limitada por las funciones

Aquí es necesario hacer la gráfica para ver cual es la superficie que definen y ver si está toda en zona positiva.

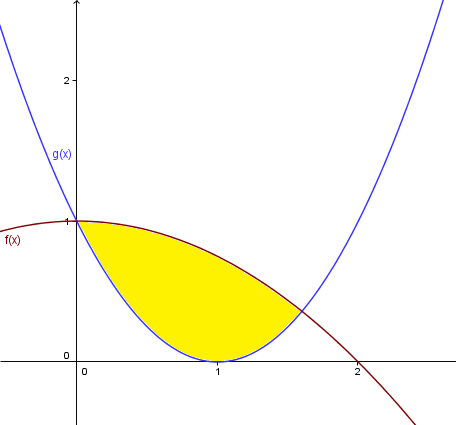
Vale, no hay problemas porque toda la superficie está en la zona positiva.

Las funciones se cortan en x=0 por la izquierda y por la derecha no está tan claro, tendremos que calcularlo.

$$\begin{align}&1-\frac{x^2}{4} = (x-1)^2\\ &\\ &\\ &1-\frac{x^2}{4}= x^2-2x +1\\ &\\ &\frac{5x^2}{4}-2x=0\\ &\\ &x=0\\ &\\ &\frac{5x}{4}-2= 0\\ &\\ &\frac{5x}{4}=2\\ &\\ &x = \frac{2·4}{5}= 8/5\end{align}$$

Y el área comprendida entre las dos es la integral de la diferencia entre los puntos x=0 y 8/5

La que está por encima es f(x) luego se le resta g(x)

$$\begin{align}&Area=\int_0^{8/5}\left(1-\frac{x^2}{4}-(x-1)^2\right)dx=\\ &\\ &\int_0^{8/5}\left(1 - \frac{x^2}{4}-x^2+2x-1  \right)dx=\\ &\\ &\int_0^{8/5}\left(- \frac{5x^2}{4}+2x  \right)dx=\\ &\\ &\left[-\frac{5x^3}{12}+x^2  \right]_0^{8/5}=-\frac{5·8^3}{12·5^3}+\frac{64}{25}=\\ &\\ &-\frac{2560}{1500}+\frac{64}{25}= -\frac{128}{75}+\frac{64}{25}=\\ &\\ &\frac{-128+192}{75}= \frac{64}{75}\\ &\end{align}$$

Y eso es todo.