Calcular el área entre curvas respecto a la variable y
Calcular el área entre curvas respecto a la variable y dadas las siguientes funciones, graficar:
y=x, y=3x, x+y=4
1 Respuesta
No entiendo del todo la pregunta, podrías concretarla más.
¿Es el área entre la curva y el eje X o la curva y el eje Y?
En caso de que quieran que el área sea una función de y, no nos dicen desde que punto empieza a contar el área.
Por supuesto no puede ser el área entre las tres rectas ya que dos de ellas son paralelas y no tienen cierre, luego pienso que son tres ejercicios independientes.
Ante la falta de claridad del texto solo tú puedes saber como habéis hecho ejercicios similares para decírmelo.
Hola, muchísimas gracias por la respuesta, en realidad, se trata de una serie de ejercicios en la que me piden calcular el área entre dos funciones, en unas me dan los límites superiores e inferiores y en otras no, así que para obtenerlos, debo calcularlos mediante una igualación entre las dos funciones y ya obtenidos,hacer la gráfica correspondiente y obtener el área mediante integración, sólo me faltó ésta de las 10 que me piden, pero no tengo una idea de cómo empezar, se me pide especificar el eje solamente, gracias de todas maneras si puedes ayudarme, Mariella.
Si claro, así suelen ser los ejercicios normales, si no te dan límites laterales es porque las curvas determinan una región cerrada. Me confundí al hacer antes las gráficas, puse
y = x-4 en lugar de
y=4-x
Y por eso me salían paralelas y pensaba que estaba mal el enunciado.
Te hago la gráfica para que veas cuál es la región que hay que calcular el área, con el quedará todo claro.
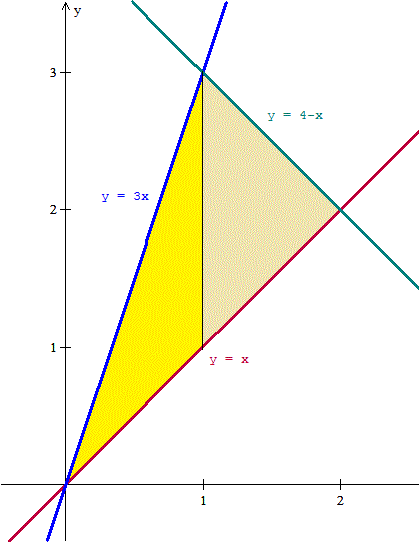
Debemos calcular el área como suma de dos áreas. Aunque en el dibujo se ven perfectamente los límites los calcularemos analíticamente, hay otros ejercicios donde no esta tan claro y hay que hacerlo analíticamente
El límite inferior de la primera región es la intersección de las rectas
y=x
y=3x
x=3x
4x=0
x=0
El límite superior de la primera e inferior de la segunda es la intersección de las rectas
y=3x
y=4-x
3x=4-x
4x=1
x=1
Y el límite superior de la segunda es la intersección de
y=4-x
y=x
4-x=x
4=2x
x=2
$$\begin{align}&A=\int_0^1 (3x-x)dx+\int_1^2(4-x-x)dx=\\ &\\ &\int_0^12xdx+\int_1^2(4-2x)dx=\\ &\\ &\\ &\left[x^2\right]_0^1 + \left[4x-x^2 \right]_1^2=\\ &\\ &\\ &1+8-4-4+1=2\end{align}$$Y eso es todo, espero que sea lo que pedían y lo hayas entendido.
Es que dicen calcular el área respecto a la variable y dadas las siguientes funciones. Es algo que no está bien expresado, el área es el área y es independiente de una variable. Lo que si cambia si es respecto a una u otra variable es la integral que se utilice, aunque el resultado tendrá que ser el mismo. Si quieres hacerlo con las integrales respecto a la variable "y" dímelo.
