Ayuda con ejercicio de derivadas

$$\begin{align}&y=2-2x-3x^{2/3}\\ &\\ &y'=-2-2x^{-1/3}=-2-\frac{2}{\sqrt[3]{x}}\\ & No \ derivable \ en \ x=0\\ &\\ &y'=0 \Rightarrow -2-\frac{2}{\sqrt[3]{x}}=0 \Rightarrow-2=\frac{2}{\sqrt[3]{x}}\\ &\sqrt[3]{x}=-1 \Rightarrow  x=-1\\ &Intervalos \ crecimiento:\\ &(-\infty,-1) f'(-10)0 \Rightarrow creciente\\ &(0,+\infty)f'(10)<0\Rightarrow decreciente\\ & Mínimo \ relativo (-1,f(-1))=(-1,1)\\ &Punto \ no \ derivable (0,2)   "picos"\\ &\\ &Concavidad:\\ &f''(x)=\frac{2}{3}x^{-4/3} \Rightarrow \frac{2}{3\sqrt[3]{x^4}}=0\Rightarrow \sin \ soluci\\ &No \ hay \ puntos \ de \ inflexión\\ &Intervalos \ concavidad-convexidad:\\ &(-\infty,0) \\ &(0,\infty) \\ &y''>0  \ para \ todo \ x\ \Rightarrow cóncaca hacia \ arriba \ siempre\\ &\\ &b) Teorema \ Lagrange  \ o \ Valor \ Medio\\ &f(x)contínua en [0,8]\\ &f(x)derivable \ en (0,8)\\ &Existe \ c \in(0,8) \ tal \ que  \ la \ recta \ tangente\ es \ paralela \ a \ la \ secante\\ &que \ pasa \ por \ (0,f(0)) y (8,f(8))\\ &f(0)=2\\ &f(8)=-26\\ &m_{secante}=\frac{-26-2}{8-0}=\frac{-7}{2}\\ &m_{tangente}=f'(x)\\ &-2-\frac{2}{\sqrt[3]{x}}=\frac{-7}{2}\\ &\\ &-\frac{2}{\sqrt[3]{x}}=2+\frac{-7}{2}\\ &-\frac{2}{\sqrt[3]{x}}=-\frac{3}{2}\\ &\\ &{\sqrt[3]{x}}=\frac{4}{3}\\ &\\ &x=\frac{64}{27} \in(0,8)\\ &\\ &\\ &\\ &\\ &\end{align}$$

Hola Gera Gorgoretti!!

a) Para los intervalos de crecimiento necesitamos los puntos críticos y'=0 y los puntos no derivables.

(Esto iba en la cabecera!)

Graficando

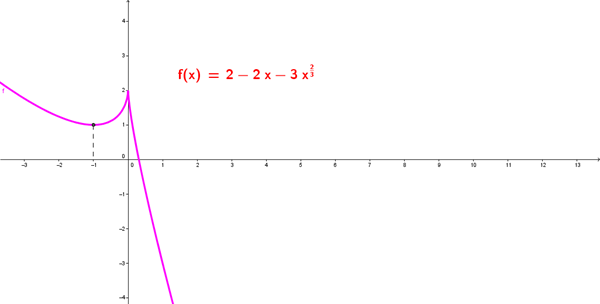
Para los intervalos de concavidad necesitaremos los puntos de inflexión (y''=0) y los puntos no derivables.

Vamos allá: