Buen día tengan todos, alguien gusta apoyar a su servidor en la solución de este ejercicio de integrales?
En base al siguiente enunciado, referente al tema de integrales se pide calcular la presión ejercida a una placa, espero contar con su valioso apoyo, quedo al pendiente de sus comentarios.
- Se tiene una placa metálica de 1 m^2 a la cual se le ejerce presión dependiente únicamente de la longitud x de un lado de la placa. De acuerdo con lo anterior, la presión sobre una franja de grosor dx viene dada por:
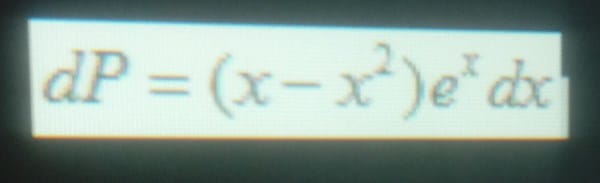
Por lo que la presión total de la placa estará dada por la siguiente integral:
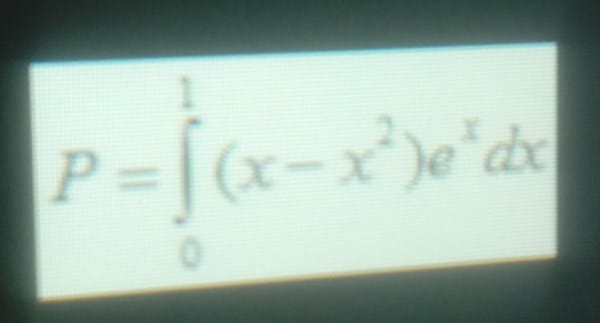
Calcula la presión ejercida en la placa.
Les deseo un excelente día y dios los cuide y bendiga,
1 respuesta
Respuesta de Valero Angel Serrano Mercadal
2
·
Este ejercicio corresponde a la temporada que estuve de baja en la página, lo veo ahora que he mirado a ver si tenías otras preguntas pendientes, puede que ya no te sirva pero...
$$\begin{align}&\text{En las integrales por partes es más comodo}\\&\text{deajar los límites para el final}\\&\\&\int(x-x^2)e^xdx=\\&\\&u=x-x^2\qquad du=(1-2x) dx\\&dv=e^x dx\qquad v=e^x\\&\\&=(x-x^2)e^x -\int(1-2x)e^x dx=\\&\\&(x-x^2)e^x-e^x+\int2xe^xdx=\\&\\&u=2x\qquad\quad du=2dx\\&dv=e^xdx\qquad v=e^x\\&\\&(x-x^2-1)e^x+2xe^x -2\int e^xdx=\\&\\&\text{Y automaticamente evaluamos el}\\&\text{resultado aunque el simbolo de}\\&\text{igualdad que he puesto sea falso,}\\&\text{cosas mucho peores se hacen en una pizarra}\\&\\&(3x-x^2-3)e^x\bigg|_0^1 = (3-1-3)e+3e^0=3-e\end{align}$$Y eso es todo.
