·
El paso es la longitud del intervalo entre el número de divisiones que hacemos
paso = (6-2)/n = 4/n
Hagamos la suma inferior, la que toma los valores de la función en el lado izquierdo.
El valor de la x en el intervalo i-esimo es
x_i = 2 + 4i/n
y el valor de la función será
f(x_i) = 2 + 4i/n + 4 = 6 + 4i/n
Con lo cual el sumatorio de los valores de la función por el paso es
$$\begin{align}&S_n = \sum_{i=0}^{n-1}\frac 4n\left(6+\frac {4i}{n} \right)=\\&\\&\text{los factores constantes salen fuera}\\&\\&=\frac 4n \sum_{i=0}^{n-1}\left(6+\frac {4i}{n} \right)=\\&\\&\text{los sumandos constantes salen multiplicados por n}\\&\\&=\frac 4n \left(6n+ \frac 4n\sum_{i=0}^{n-1}i \right)=\\&\\&24 + \frac {16}{n^2}\sum_{i=0}^{n-1}i=\\&\\&\text{por la fórmula de la suma de sucesiones aritméticas}\\&\\&=24 + \frac{16}{n^2}·\frac{n(n-1)}{2}=\\&\\&=24 + \frac{8n^2-8n}{n^2}=\\&\\&=24 +8 -\frac 8n =\\&\\&= 32 -\frac 8n\\&\\&\text{y la suma Riemann es el límite cuando n}\to\infty\\&\\&S_{\infty}=\lim_{n\to\infty} \left(32-\frac 8n\right)= 32\end{align}$$Lo comprobamos sabiendo que la integral es (x^2)/2 + 4x entre 2 y 6
36/2 + 24 - 2 - 8 = 18+24 -10 = 32
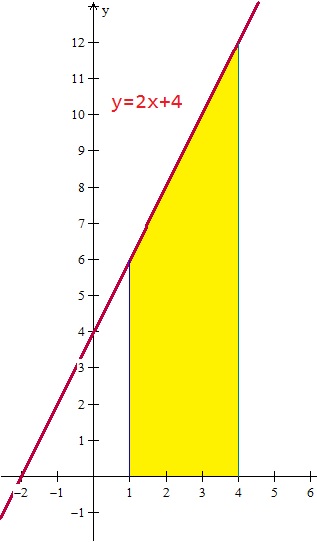
Y la gráfica es esta:
Y eso es todo.

