Resolución de problemas sobre Teorema fundamental de cálculo (5)
Ayuda por favor !, gracias
a) Usa la siguiente tabla la cuál te será útil para resolver los problemas, recuerda que no debes considerar la constante “C” ya que nuestra integral si se encuentra definida.
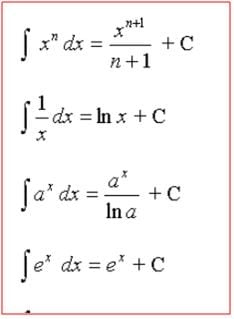
b) Recuerda que todos los resultados tendrán un valor numérico pues estamos calculando áreas y las unidades serán u² (unidades al cuadrado).
5.
$$\begin{align}&\int_2^4(x^3+x^2)dx\end{align}$$
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1
·
Usaremos la primera fórmula pero antes descompondremos en dos la integral (aunque no es necesario) para decir que la usamos tal como aparece.
$$\begin{align}&\int_2^4(x^3+x^2)dx= \int_2^4 x^3 dx+\int_2^4x^2dx=\\&\\&\left. \frac{x^{3+1}}{3+1}\right|_2^4 + \left.\frac{x^{2+1}}{2+1}\right|_2^4=\left. \frac{x^{4}}{4}\right|_2^4 + \left.\frac{x^{3}}{3}\right|_2^4=\\&\\&\frac{4^4}{4}-\frac{2^4}{4}+ \frac{4^3}{3}-\frac{2^3}{3}=\\&\\&\frac{256-16}{4}+\frac{64-8}{3}= \frac{240}{4}+ \frac{56}{3}=\\&\\&60 + \frac{56}{3}= \frac{60·3+56}{3}= \frac{180+56}{3}=\frac{236}{3}\end{align}$$Ahora me he fijado en la nota b), hasta ahora nolo había hecho. Pues si el profesor acostumba a poner u² después de las respuestas ponlo. La verdad es que las integrales definidas no solo sirven para calcular áreas, y no se suele poner nada, pero ponlo.
