Como puedo resolver esta integral
Determina la integral de la siguiente función (Nota: Usted debe determinar el método de integración que corresponda.
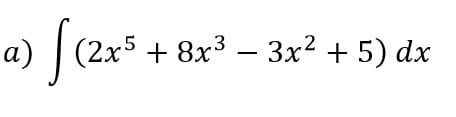
2 respuestas
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal
1
