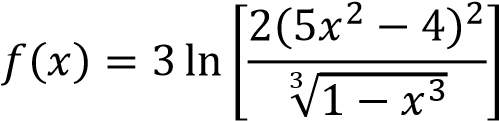$$\begin{align}& \end{align}$$¡Hola Jacobo!
·
Estas derivadas a lo mejor no quedan bien por la poca anchura del editor y lo grande que queda la letra, pero vamos.
$$\begin{align}&f(x) =3ln\left[\frac{2(5x^2-4)^2}{\sqrt[3]{1-x^3}} \right] \\&\\&\text{resolverla así es muerte segura}\\&\\&f(x) = 3\left(ln[2(5x^2-4)^2] - ln(\sqrt[3]{1-x^3})\right)=\\&\\&3\left(ln2 +2ln(5x^2-4) -\frac 13ln(1-x^3)\right)=\\&\\&3ln2+6ln(5x^2-4)-ln(1-x^3)\\&\\&f'(x) =\frac{6·10x}{5x^2-4}-\frac{-3x^2}{1-x^3}=\\&\\&\frac{60x}{5x^2-4}+\frac{3x^2}{1-x^3}\\&\\&\text{yo entiendo que con esto ya está bien simplificada}\\&\text{otra forma sería}\\&\\&f'(x)=\frac{60x(1-x^3)+3x^2(5x^2-4)}{(5x^2-4)(1-x^3)}=\\&\\&\frac{60x-60x^4+15x^4-1x^2}{5x^2-5x^5-4+4x^3}=\\&\\&\frac{-45x^4-12x^2+60x}{-5x^5+4x^3+5x^2-4}\\&\\&\text {o para los que no quieren coeficientes directores negativos}\\&\\&f'(x)=\frac{45x^4+12x^2-60x}{5x^5-4x^3-5x^2+4}\\&\\&\text{o para los que no renuncian a un último factor común}\\&\\&f'(x)=\frac{3x(15x^3+4x-20)}{5x^5-4x^3-5x^2+4}\end{align}$$En fin, la forma final de presentarlo es lo de menos, lo importante ha sido simplificar la función inicial con las propiedades de los logaritmos, si no ya te decía.
En memoria del hermano Juanjo y esas integrales del arco tangente de una raíz cuadrada con cientes de cosenos que era la tangente del ángulo doble y se resolvía inmediatamente si sabías simplificar antes. Pero es que aun no habíamos dado esa parte de la trigonometría. JaJa!
·
Y eso es todo.