Calcule las siguientes integrales: a) ∫▒〖2x^2 (7-3x^3 )^5 〗 dx
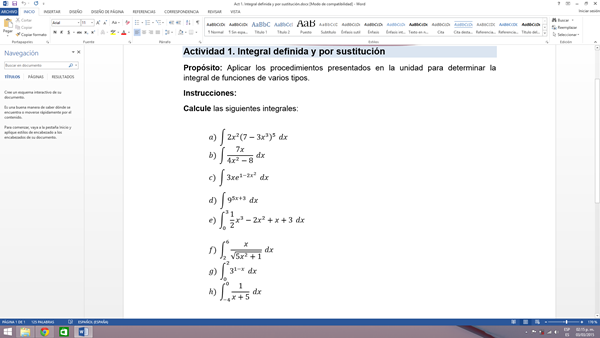 me ayudan a resolver estas integrales , gracias, ya que no les entiendo muy bien, saludos
me ayudan a resolver estas integrales , gracias, ya que no les entiendo muy bien, saludos
2 respuestas
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal
1
