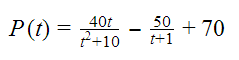Para las funciones determina el límite indicado en cada una, realizando los procedimientos correspondientes.
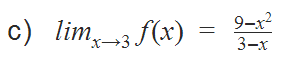
Ya me habian ayudado con este ejercicio, pero me dicen lo siguiente al momento de revisarlo. Esta es la primera solución que se había respondido.
Este tiene interés, si lo evaluamos da 0/0
(9 - 32) / (3-3) = (9-9) / (3-3) = 0 / 0
Y lo que se debe hacer es simplificar factores con valor 0 del numerador y denominador.
En este caso tenemos en el numerador la fórmula de un producto notable
a2−b2=(a+b)(a−b)
Luego
9−x2=(3+x)(3−x)
y el límite es
limx→39-x23-x=limx→3(3+x) (3-x)3-x=
limx→3(3+x) = 3+3 = 6
y esto las indicaciones al momento de evaluar:
Con respecto a tu evidencia tienes mal el inciso c del tercer punto, al dividir entre infinito lo calculas como cero y no es así.. Es infinito.
Ante todo debes tener en cuenta que todo número sumado con ∞ te dará siempre ∞, al igual que todo número dividido entre ∞ te dará ∞.
1 Respuesta
·
¿Me puedes decir que graduado, diplomado o licenciado te ha dicho eso?
Si la corrección se refiere al ejercicio que has puesto se le ha debido ir la olla, no encuentro otra explicación, no hay ningún infinito en la expresión esa, como no lo haya confundido con el 3 no le encuentro ninguna explicación. La verdad es que lo veo muy surealista. ¿Estás seguro que se refiere a este límite? ¿No será otro? En todo caso si es un límite que te he resuelto yo, el equivocado es el corregidor con casi total seguridad.
Un urbanista de la ciudad determina un modelo matemático de la población P (en miles de personas), de la comunidad, en términos (o en función), del tiempo t (en años). Esta se expresa como:
Este seria el otro inciso C
c)¿Qué población esperaría el urbanista en el largo plazo?
(y aqui la observacion del docente) con respecto a tu evidencia tienes mal el inciso c del tercer punto, al dividir entre infinito lo calculas como cero y no es así.. es infinito.
Ante todo debes tener en cuenta que todo número sumado con ∞ te dará siempre ∞, al igual que todo número dividido entre ∞ te dará ∞.
Ves, ya decía yo que ese límite no podía ser. ¿Pero este te lo resolví yo o lo resolviste tú? En cualquiera de los casos necesito ver como se resolvió. Si lo hice yo mándame el enlace a la pregunta que respondí.
Que tal Sr, Valero esta es la solución que había checado, no recuerdo si la tome de alguna respuesta que alguien más había hecho con el mismo problema.
No es ese mi estilo, yo jamás escribiría
70,000
Escribiría
70000
Aunque la frase:
"En los límites en el infínito, cuando el grado del denominador es mayor que el del numerador, el límite es 0"
Es completamente mía y completamente cierta.
Si el docente no sabe esa cosa tan simple es problema suyo.
Si acaso habría que concretar más para que sea ultracorrecta, pero por el contexto donde se decía era correcta.
La frase sería el límite en más infinito o menos infinito de una función racional (cociente de dos polinomios) cuyo grado del denominador es mayor que el del numerador es 0.
Y eso es una verdad inamovible.
Por eso el límite de P(t) es 0-0+70 = 70
Y al ser miles de personas son 70000 personas.
Es que no se puede decir otra cosa, si el docente es capaz de decir esto
"al igual que todo número dividido entre ∞ te dará ∞"
Debe ser expulsado automáticamente de la universidad y volver a hacer la carrera porque es:
"toda constante dividida entre ∞ te dará 0"
