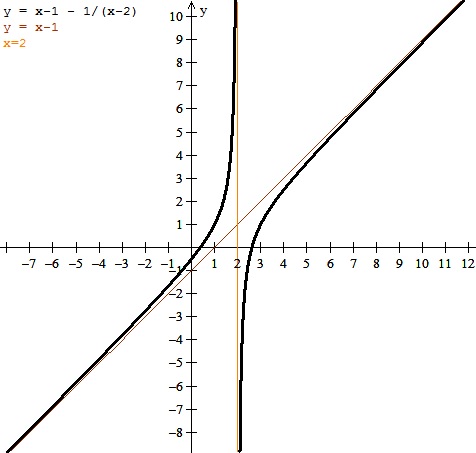Como graficar ràpidamente estas funciònes, sin tabular?

·

No sé a qué se refieren con rápidamente, si no se puede tabular hay que calcular unas cuantas cosas y eso de rapidez no tiene nada. Tal vez hayáis dado algún método especial, si es así yo no tengo ni idea y tú si.

En todo caso haré solo una en esta pregunta, la otra la mandas en otra pregunta.

Voy a ver primero como puede quedar la función

$$\begin{align}&y=x-1-\frac{1}{x-2}=\\&\\&\frac{x^2-2x-x+2-1}{x-2}=\frac{x^2-3x+1}{x-2}\end{align}$$

Me parece que es peor el remedio que la enfermedad.

Bueno, en x=2 tenemos una asíntota vertical eso está claro. Veamos cuál es el signo del numerador en x=2

2^2-3·2+1 = -1

Entonces a la izquierda del 2 será negativo entre negativo y tendera a infinito y a la derecha a -infinito.

Otra cosa que se puede calcular son los cortes con el eje X

$$\begin{align}&x^2-3x+1=0\\&\\&x=\frac{3\pm \sqrt{9-4}}{2}=\frac{3\pm \sqrt 5}{2}\\&\\&x_1=0.38196601125011\\&x_2=2.618033988749895\end{align}$$

Y el corte con el eje Y es

y = 0-1 - 1/(0-2) = -1+1/2 = 1/2

Podemos ver también otra cosa, que en el infinito el sumando 1/(x-2) tiende a 0 y la función se quedaría en

y=x-1

Entonces esa recta y=x-1 es la asíntota oblicua de la función.

Pues yo pienso que con esto podría valer para hacer un dibujo rápido y nos dejamos de máximos, mínimos, decrecimiento, etc. Porque no nos van a decir nada o lo que nos digan se puede deducir de lo que tenemos. Dibujando la asíntota, los cortes con los ejes y sabiendo que en 2 por la izquierda tira a infinito y por la derecha a - infinito es suficiente

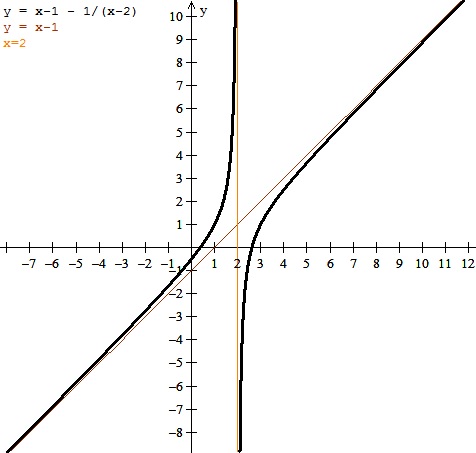
Y eso es todo.