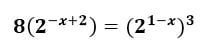Como resolver la siguiente ecuación?
Me ayudan por favor con resolver la siguiente ecuación:
Les Agradezco de antemano
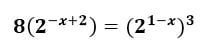
1 Respuesta
Respuesta
1
Me ayudan por favor con resolver la siguiente ecuación:
Les Agradezco de antemano