Calcular el área en que una parábola corta a un círculo

$$\begin{align}& \end{align}$$

¡Hola Ninel!

·

Hagamos la gráfica para mayor seguridad.

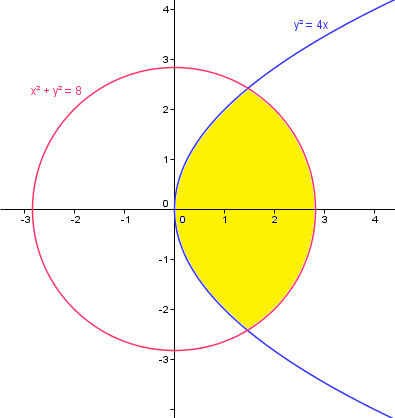
Podemos expesar esa área como una sol integral de la diferencia de dos funciones si tomamos fijos los límites de y. Vamos a calcular las coordenadas y de los puntos de corte

4x = y^2  ==> x= y^2 / 4

x^2 + y^2 = 8  ==>

y^4 /16 + y^2 = 8 ==>

y^4 + 16y^2 - 128 =0

$$\begin{align}&y^2=\frac{-16\pm \sqrt{256+512}}{2}=\\&\\&\frac{-16\pm16 \sqrt {3}}{2}= -8\pm 8\sqrt {3}\\&\\&\text{como eso es }y^2 \text{ debe ser positivo}\\&\text{solo sirve la del signo +}\\&\\&y^2 = 8\sqrt 3-8\\&\\&y=\pm \sqrt{8 \sqrt 3-8}\approx 2.42\end{align}$$

Y si tomamos en y los límites de integración lo que se debe integrar es la diferencia de dos funciones de y, o sea de la forma x=f(y)

$$\begin{align}&x=\frac{y^2}4  \quad\text{es la inferior}\\&\\&x=\sqrt{8-y^2} \quad\text{es la superior}\\&\\&A=\int_{-\sqrt{8 \sqrt 3-8}}^{\sqrt{8 \sqrt 3-8}}\left(\sqrt{8-y^2}-\frac{y^2}{4}\right)dy\end{align}$$

¿Puedes continuarla tú?  Ya te digo que no será fácil.